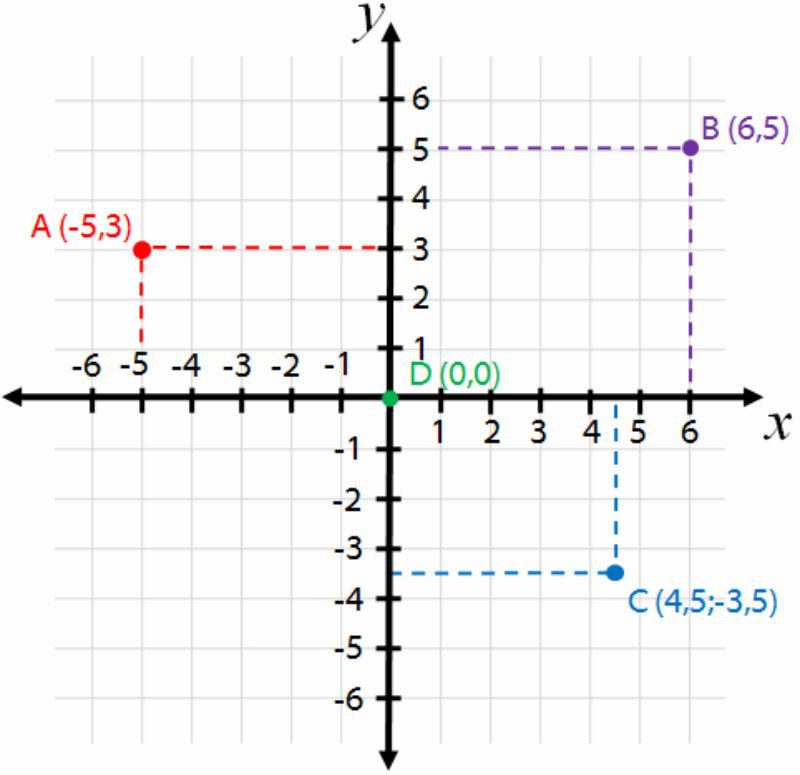
O plano cartesiano é um objeto matemático plano e composto por duas retas numéricas perpendiculares, ou seja, retas que possuem apenas um ponto em comum, formando um ângulo de 90°. Esse ponto comum, é um conhecido como origem e é nele que é marcado o número zero de ambas retas. O plano cartesiano recebeu esse nome por ter sido idealizado por Renê Descartes e é usado fundamentalmente para sistematizar técnicas de localização no plano. As duas retas que dão origem ao plano cartesiano precisam ser retas numéricas, pois essa é a condição que tornará possível encontrar localizações de pontos quais quer no plano. Essa localização é a base fundamental de muitos conhecimentos comuns no cotidiano, como distância entre pontos.
ATIVIDADE 1
Construa no seu caderno um sistema cartesiano e nele marque os pontos: A (1,1), B ( 0,0), C ( -2, 2 ), D (-1,-1) e E ( -2.-2).
ATIVIDADE 2
Lembrando que uma equação do 10 grau com duas variáveis, é uma equação do 10grau, na qual aparecem duas letras, as quais nós chamamos de variáveis ou incógnitas.
Ex. 2x + 2y = 6 . Aqui as duas variáveis são x ey.
Chamamos de representação geométrica de uma reta, a representação no sistema cartesiano, (sistema X o Y), da referida reta.
Para fazer a representação geométrica de uma equação do 1 grau de duas, inicialmente construímos uma tabela de forma que você atribui um determinado valor para x, usando a equação, você encontra o valor correspondente de y. É importante saber que sempre a representação geométrica, ou falando de outra forma, a representação no sistema cartesiano de uma equação com duas variáveis do 1 o grau é sempre uma reta.
Recomendo assistir os seguintes vídeos no youtube:
Veja:
A representação geométrica da reta: 2x+2y = 6
| x | 2x + 2y = 6 | ( x, y ) |
| 2 | 2.( 2) + 2y = 6 4 + 2y=6 2y= 6 – 4 2y =2 y = 1 | ( 2, 1) |
| 0 | 2. (0)+ 2y= 6 0+2y= 6 y= 3 | ( 0, 3) |
| -2 | 2.( -2) + 2y = 6 – 4 + 2y=6 2y= 6 + 4 2y =10 y = 5 | ( – 2, 5) |
Agora é só construir os eixos XOY, representar nele os pontos (2,1),(0,3) e
(- 2, 5). e traçar a reta: 2x + 2y= 6.
Agora faça você no seu caderno, a representação da equação x + y = 3 no plano cartesiano (é o mesmo que representação geométrica da reta).
ATIVIDADE 3
Essa atividade é a solução gráfica de um sistema de duas equações,com duas incógnitas do 1o grau. Para tanto você fará a representação geométrica de cada uma das equações do sistema e a solução geométrica desse sistema será o ponto de encontro dessas retas. Lembreque no sistema cartesiano, cada ponto é representado por letra maiúscula, e por um par ordenado ( x,y).
Para um melhor entendimento veja o vídeo :
Agora faça você no caderno a representação geométrica do sistema:
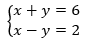
Saiba Mais | Referências:
SILVEIRA, Enio e MARQUES, Cláudio. Matemática compreensão e prática. São Paulo: Moderna 2017; IEZZI, Gelson; DOLCE, Osvaldo; MACHADO, Antonio. Matemática e Realidade. São Paulo: Atual, 2019.
| Objeto de Conhecimento | Valor numérico de expressões algébricas Associação uma equação linear de 1° grau a uma reta no plano cartesiano. |
| Habilidades | (EF08MA07) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano. (EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso. |
| Proponentes/ Professores: | Sheila Jeremy de Clermon Pinerolo Almeida Castro Silva |
| Instituição Educacional: | Escola Municipal Nova Conquista |
| CRE: | Maria Helena Bretas |
Ciclo da Adolescência – Turma H (8º ano) – Ed. Financeira e Empreendedorismo