Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.
Disponível em: <Matemática Geometria Triângulo – Foto gratuita no Pixabay> Acesso em 08 de novembro de 2022.
O Teorema de Pitágoras é um dos mais famosos e fundamentais conceitos da matemática, cuja descoberta é atribuída ao matemático grego Pitágoras, por volta do século VI a.C. Ele estabelece uma relação entre os lados de um triângulo retângulo, ou seja, um triângulo que possui um ângulo reto (90 graus).
O contexto histórico em que o Teorema de Pitágoras foi formulado é envolto em lendas e mistérios, mas sua importância e aplicabilidade transcendem os séculos, permanecendo relevante até os dias de hoje.
A definição do Teorema de Pitágoras afirma que
“Em um triângulo retângulo, o quadrado do comprimento da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos comprimentos dos outros dois lados.”
Matematicamente, isso pode ser expresso como:
Imagem do autor produzido no canva
Onde:
- b e c representam os comprimentos dos catetos (os lados que formam o ângulo reto) e
- a é o comprimento da hipotenusa.
Essa relação tem inúmeras aplicações práticas em situações do dia a dia. Por exemplo:
- Imagine que você precise calcular a distância mais curta entre dois pontos em um mapa, mas só pode se mover ao longo de ruas que formam ângulos retos. Isso cria uma série de triângulos retângulos, e o Teorema de Pitágoras pode ser utilizado para determinar a distância mais curta, que é a hipotenusa desses triângulos.
- Imagine que você esteja construindo uma cerca e precisa garantir que ela esteja perfeitamente reta. Você pode usar o Teorema de Pitágoras para verificar se os cantos estão formando ângulos retos, medindo as diagonais e comparando-as com as medidas dos lados. Se as medidas estiverem de acordo com a relação do teorema, então os ângulos são retos e a cerca está corretamente alinhada.
Além disso, o teorema é fundamental em áreas como a engenharia, arquitetura, física e astronomia. Por exemplo, na engenharia civil, ao projetar estruturas como pontes ou edifícios, os engenheiros frequentemente precisam garantir que os ângulos estejam corretos para evitar falhas estruturais. O Teorema de Pitágoras é essencial para esses cálculos.
Um exemplo simples para finalizar
Um triângulo retângulo tem um dos catetos medindo 3 unidades e a hipotenusa medindo 5 unidades. Qual é o comprimento do outro cateto?
Resolução:
Podemos usar diretamente o Teorema de Pitágoras, que afirma que em um triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Seja “a” o cateto dado (3 unidades) e “c” a hipotenusa (5 unidades). O outro cateto é representado por “b”.
a2 + b2 = c2
Substituindo os valores conhecidos:
32 + b2 = 52
9 + b2 = 25
Subtraindo 9 de ambos os lados:
b2 = 16
Tomando a raiz quadrada em ambos os lados para encontrar “b”:
b = 4
Portanto, o comprimento do outro cateto é 4 unidades.
Ficamos por aqui, até o próximo.
Questão 1
Uma piscina retangular mede 24 m de comprimento por 18 m de largura. Quanto mede a diagonal dessa piscina?
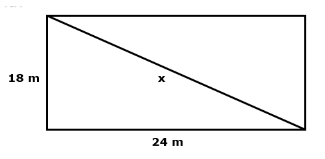
Imagem do arquivo pessoal
Questão 2
Ana tem uma área com telhado assimétrico e deseja cobrir a frente para diminuir a passagem de sol. Na construção desse telhado os banzos superiores medem 8 metros e 6 metros. E essa estrutura forma um triângulo retângulo, como mostra a imagem:

Imagem do arquivo pessoal
A) Qual a medida da base desse triângulo?
B) Qual é a altura desse triângulo?
Questão 3
Um engenheiro está projetando um novo telhado para uma casa. Ele precisa garantir que as diagonais do telhado sejam corretas para evitar problemas estruturais. Para isso, ele utiliza o Teorema de Pitágoras para verificar os ângulos retos. Se uma das diagonais do telhado mede 15 metros, e uma lateral mede 12 metros, podemos afirmar que o comprimento da outra lateral é igual a
(A) 9 metros.
(B) 8 metros.
(C) 10 metros.
(D) 11 metros.
Questão 4
Um agricultor está construindo um cercado para seu gado, usando a parede da fazenda como um dos lados, que mede 20 metros. Ele deseja calcular corretamente o comprimento do outro lado para garantir a segurança do cercado, sabendo que a diagonal entre esses dois lados mede 25 metros. Dessa forma, o comprimento exato do outro lado do cercado será
(A) 15 metros.
(B) 18 metros.
(C) 21 metros.
(D) 22 metros.
| Autoria | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades estruturantes: | (EF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos.(EF09MA14-B) Ler, interpretar, resolver e elaborar problemas de aplicação do Teorema de Pitágoras ou das relações de proporcionalidade, envolvendo retas paralelas cortadas por secantes. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender sempre. 9°. Ano – Ensino Fundamental; Língua Portuguesa e Matemática; 4°. Bimestre; Goiânia, 2022. |

