Esta atividade de Matemática, tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.

Disponível em: < a href=’https://br.freepik.com/fotos-vetores-gratis/monumento’>Monumento foto criado por wirestock – br.freepik.com</a>Acesso em 07, maio 22.
Tales de Mileto foi um dos mais notáveis filósofos e matemáticos da Grécia Antiga. Ele contribuiu significativamente para o desenvolvimento da geometria e foi um dos pioneiros na compreensão da semelhança de triângulos.
A compreensão da semelhança de triângulos permitiu a Tales resolver problemas práticos, como a determinação de alturas inacessíveis, por meio da utilização de triângulos semelhantes.
Tales notou que quando um feixe de raios de sol incide em duas hastes verticais, formando sombras no chão, a proporção entre o comprimento das sombras e o comprimento das hastes permanece constante, independentemente da altura do sol. Essa observação o levou a compreender a propriedade fundamental da semelhança de triângulos.
Esse conceito foi imprescindível para o desenvolvimento de muitas áreas da matemática e da física, como a trigonometria, a geometria analítica e a geometria espacial. E também teve aplicações práticas em áreas como a topografia, engenharia e arquitetura.
A semelhança de triângulos descreve a relação entre dois triângulos que possuem ângulos congruentes e lados proporcionais. Essa propriedade permite estabelecer correspondências entre os elementos dos triângulos e facilita o estudo de suas propriedades e medidas. Para que dois triângulos sejam considerados semelhantes, é necessário que os ângulos correspondentes sejam iguais e que os lados correspondentes estejam em proporção.
Essa proporção entre os lados é chamada de razão de semelhança. Em outras palavras, se os ângulos de um triângulo são iguais aos ângulos correspondentes de outro triângulo, então os lados desses triângulos são proporcionais.
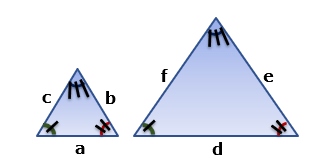
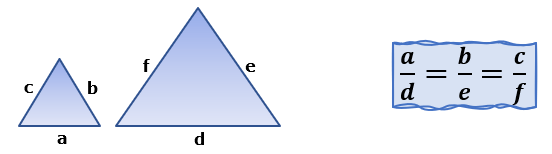
Existem três casos principais em que podemos afirmar que dois triângulos são semelhantes. Esses casos são conhecidos como AA (ângulo-ângulo), LAL (lado-ângulo-lado) e LLL (lado-lado-lado). Cada caso envolve condições específicas que devem ser satisfeitas para que os triângulos sejam considerados semelhantes.
1° caso: No caso AA (ângulo-ângulo), dois triângulos são semelhantes se possuem dois ângulos correspondentes congruentes. Isso significa que, se dois triângulos têm os mesmos ângulos, mesmo que os tamanhos dos lados sejam diferentes, eles ainda serão considerados semelhantes.
2° caso: No caso LAL (lado-ângulo-lado), dois triângulos são semelhantes se possuem um lado proporcional a um ângulo correspondente e outro lado proporcional a outro ângulo correspondente. Isso significa que a razão entre os comprimentos dos lados correspondentes deve ser a mesma. Nesse caso, a semelhança é determinada tanto pelos ângulos quanto pelos lados.
3° caso: No caso LLL (lado-lado-lado), dois triângulos são semelhantes se possuem todos os lados proporcionais. Então, os casos de semelhança de triângulos, como o AA, LAL e LLL, são condições que determinam quando dois triângulos são considerados semelhantes. Esses casos são baseados em relações entre ângulos correspondentes e/ou lados proporcionais.
Assista a videoaula abaixo da professora Priscilla com essa temática.
Sabendo isso, responda a atividade abaixo:
Questão 1
Para descobrir a altura de um poste, Maria mediu a sombra do poste, em seguida, mediu sua própria sombra. A sombra do poste tinha 5 metros, e a de Maria, que tem 1,6 metros de altura, tinha 2 metros. Qual a altura desse poste?
(A) 2 metros
(B) 3 metros
(C) 4 metros
(D) 5 metros
Questão 2
Para medir a largura aproximada de um rio, foi utilizado o esquema mostrado na figura:

Disponível em: < a href=’https://br.freepik.com/fotos-vetores-gratis/rio-agua’>Rio agua vetor criado por upklyak – br.freepik.com</a>Acesso em 07, maio 22.
Então, a largura desse rio mede aproximadamente:
(A) 16 metros.
(B) 24 metros.
(C) 20 metros.
(D) 15 metros.
Questão 3
Verifique se os triângulos a seguir são semelhantes e justifique sua resposta:

Imagem do arquivo pessoal
Questão 4
Usando exemplos explique quais são os casos em que podemos afirmar que dois triângulos são semelhantes.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidade: | (EF09MA12-A) Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes. (EF09MA12-B) Reconhecer triângulos semelhantes em situações de ampliação, congruência e redução, e as relações que existem entre seus perímetros e suas áreas. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender sempre. 9°. Ano – Ensino Fundamental; Língua Portuguesa e Matemática; 2°. Bimestre; Goiânia, 2022. |

