Esta atividade de Matemática, tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 8º ano do Ensino Fundamental.

Disponível em: <http://www.sfbbrasil.org/gifs/jogosdoazar.jpg >Acesso em 20, abril 22.
A probabilidade é uma medida numérica que quantifica a chance associada a um evento. Ela expressa a quantidade de vezes que um evento específico pode ocorrer em relação ao número total de resultados possíveis em um experimento aleatório. Em outras palavras, a probabilidade é uma medida de quão provável é que um evento ocorra em relação ao conjunto de todos os resultados possíveis.
Evento: Um evento é um resultado ou conjunto de resultados de um experimento aleatório. Em outras palavras, é qualquer resultado possível que possa ocorrer em uma situação de incerteza. Por exemplo, ao lançar um dado, os eventos podem ser “obter um número par” (que inclui os resultados 2, 4 e 6) ou “obter um número ímpar” (que inclui os resultados 1, 3 e 5).
Espaço Amostral: O espaço amostral de um experimento aleatório é o conjunto de todos os resultados possíveis desse experimento. É uma lista completa de todos os resultados que podem ocorrer. Por exemplo, ao lançar uma moeda, o espaço amostral consiste em {cara, coroa}. No caso de lançar um dado de seis lados, o espaço amostral é {1, 2, 3, 4, 5, 6}.
Cálculo de probabilidade:
A probabilidade de um evento é calculada dividindo o número de resultados favoráveis pelo número total de resultados possíveis. Isso é adequado para experimentos em que todos os resultados são igualmente prováveis.
Por exemplo, ao lançar uma moeda honesta, há dois resultados possíveis: cara ou coroa. A probabilidade de obter cara é de 1/2, pois há uma chance em duas de que isso aconteça. Da mesma forma, ao lançar um dado de seis lados, há seis resultados possíveis (de 1 a 6), e a probabilidade de obter qualquer número específico é de 1/6, pois há uma chance em seis de que esse resultado ocorra.
Evento complementar:
Um evento complementar é o evento que consiste em todos os resultados que não estão incluídos em um evento específico. Em outras palavras, é o oposto ou complemento do evento original. O evento complementar sempre ocorre quando o evento original não ocorre e vice-versa.
Por exemplo, considere o lançamento de um dado de seis lados. Se definirmos o evento A como “obter um número par”, então o evento complementar de A, denotado por A’, seria “obter um número ímpar”. Em termos de resultados específicos, o evento A incluiria os números {2, 4, 6}, enquanto o evento complementar A’ incluiria os números {1, 3, 5}.
Quando consideramos um evento A e seu evento complementar A’, a soma das probabilidades desses eventos é igual a 1.
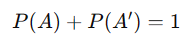
Onde:

Assista a videoaula abaixo da professora Priscilla com essa temática.
Sabendo isso, responda a atividade abaixo:
Questão 1
Imagine o lançamento simultâneo de 3 moedas e responda às perguntas:
- Qual é o espaço amostral nessa situação?
- Qual a probabilidade de se obter as três faces iguais?
Questão 2
Em um sorteio durante uma festa junina foram vendidos 200 números. Pedro comprou 5 deles. A chance de ele ganhar o prêmio é
(A) 2.5%
(B) 5%
(C) 7.5%
(D) 10%
Questão 3
No lançamento simultâneo de dois dados comuns numerados de 1 a 6, podemos afirmar que a probabilidade da soma dos valores das faces superiores ser um resultado maior do que cinco é
(A) 50%
(B) 66.67%
(C) 25%
(D) 16.67%
Questão 4
Em um experimento, um dado comum numerado de 1 a 6 é lançado duas vezes consecutivas. Qual é a probabilidade de que a soma dos valores das faces superiores seja um número par?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidade: | (EF07MA34-A) Planejar e realizar experimentos aleatórios ou simulações que envolvem cálculo de probabilidades ou estimativas por meio de frequência de ocorrências. (EF07MA34-B) Solucionar problemas que incluam noções de espaço amostral e de probabilidade de um evento, apresentando respostas por meio de representações fracionárias, decimais ou porcentagens. (EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender sempre. 8°. Ano – Ensino Fundamental; Língua Portuguesa e Matemática; 2°. Bimestre; Goiânia, 2022. |

