Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 7º ano do Ensino Fundamental.

Disponível em: <Dados Morrer Probabilidade – Gráfico vetorial grátis no Pixabay> Acesso em 05 de outubro de 2022.
A probabilidade é a chance de um evento acontecer em relação ao número total de resultados possíveis. Ela pode ser utilizada em diversos contextos da vida, desde a previsão do tempo até a análise de riscos em investimentos financeiros. Ela serve para analisar situações incertas e prever resultados futuros. Por exemplo, em um jogo de azar, entender a probabilidade de ganhar pode ajudar a decidir se vale a pena jogar. Da mesma forma, em áreas como ciência, engenharia e finanças, a probabilidade também tem muita utilidade.
Experimentos Aleatórios:
Experimentos aleatórios são processos ou eventos cujos resultados não podem ser previstos com certeza absoluta. Eles envolvem incerteza e variabilidade em relação aos resultados possíveis. Esses experimentos são caracterizados por produzir diferentes resultados cada vez que são realizados, mesmo sob as mesmas condições iniciais.
Um exemplo de um experimento aleatório é o lançamento de um dado justo. Cada vez que você lança um dado, há várias possibilidades de resultados (de 1 a 6), e não é possível prever com certeza qual número aparecerá antes do lançamento. Outros exemplos de experimentos aleatórios incluem lançar uma moeda, retirar uma carta de um baralho embaralhado, medir a temperatura em um dia específico e observar o tempo de chegada dos ônibus em uma terminal rodoviário.
Evento: Um evento é um resultado específico ou uma coleção de resultados possíveis de um experimento aleatório. Em outras palavras, é um subconjunto do espaço amostral que representa um resultado particular que estamos interessados em observar ou analisar. Por exemplo, ao lançar um dado, um evento pode ser “obter um número par” ou “obter um número ímpar”. Em um experimento de lançamento de moeda, um evento pode ser “obter cara” ou “obter coroa”. Os eventos podem ser simples, envolvendo apenas um resultado possível, ou compostos, envolvendo vários resultados possíveis.
Espaço Amostral: O espaço amostral é o conjunto de todos os resultados possíveis de um experimento aleatório. Em outras palavras, é o conjunto de todos os resultados que podem ocorrer em uma situação de interesse. Por exemplo, ao lançar um dado de seis faces, o espaço amostral é {1, 2, 3, 4, 5, 6}, pois esses são os seis resultados possíveis. No caso de lançar uma moeda, o espaço amostral é {cara, coroa}, pois há apenas dois resultados possíveis. O espaço amostral representa todas as possibilidades que precisamos considerar ao calcular probabilidades ou analisar resultados de um experimento.
Como calcular a probabilidade de um evento:
- Identificar o espaço amostral (S): Por exemplo, ao lançar um dado, o espaço amostral é {1, 2, 3, 4, 5, 6}.
- Definir o evento de interesse (E): Por exemplo, se queremos calcular a probabilidade de obter um número par ao lançar um dado, o evento E seria o conjunto {2, 4, 6}.
- Contar o número de resultados favoráveis (n(E)): Determine quantos resultados no espaço amostral correspondem ao evento de interesse. No exemplo do dado, há 3 números pares, então n(E) = 3.
- Contar o número total de resultados possíveis (n(S)): Calcule o número total de resultados no espaço amostral. No exemplo do dado, há 6 faces, então n(S) = 6.
- Calcular a probabilidade (P): Divida o número de resultados favoráveis pelo número total de resultados possíveis. A fórmula para calcular a probabilidade é:
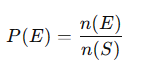
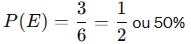
Assista a videoaula com a professora Priscilla com essa temática
Questão 1
Maria vai a um evento e tem disponíveis 3 calças (preta e azul clara e azul escura) e 4 blusas (azul, vermelha, amarela e verde). A probabilidade dela usar calça azul com blusa vermelha é
(A) 1/12.
(B) 1/6.
(C) 1/4.
(D) 1/3.
Questão 2
Imagine o lançamento simultâneo de três moedas. Responda:
- Quantos e quais são os elementos desse espaço amostral?
- Qual a probabilidade de obter três faces iguais?
- Qual a probabilidade de obter pelo menos uma “cara” nesse lançamento?
- Qual a probabilidade de ter exatamente duas faces com “coroa”?
Questão 3
João está planejando uma atividade para a festa de aniversário de seu filho. Ele quer incluir um jogo de dados, mas antes de decidir, ele se pergunta: “Qual é a probabilidade de obtermos um número par ao lançar o dado uma única vez?”
Questão 4
Mariana participou de uma rifa de Natal onde foram vendidos 500 bilhetes. Sabendo que ela adquiriu apenas 5, a probabilidade de que ela ganhe o prêmio é de
(A) 1/100.
(B) 1/125.
(C) 1/250.
(D) 1/500.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA34-A) Planejar e realizar experimentos aleatórios ou simulações que envolvem cálculo de probabilidades ou estimativas por meio de frequência de ocorrências. (EF07MA34-B) Solucionar problema que inclua noções de espaço amostral e de probabilidade de um evento, apresentando respostas por meio de representações fracionárias, decimais ou porcentagens. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |
