Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 7º ano do Ensino Fundamental.

Disponível em: <Borboleta Inseto Cromático – Gráfico vetorial grátis no Pixabay> Acesso em 05 de setembro de 2022.
O plano cartesiano, também conhecido como sistema de coordenadas cartesianas, foi desenvolvido pelo matemático e filósofo francês René Descartes no século XVII. A ideia de um sistema de coordenadas que representasse pontos no espaço de forma precisa surgiu da necessidade de resolver problemas geométricos e algébricos.
Descartes estava interessado em encontrar métodos para descrever visualmente relações matemáticas abstratas, especialmente em geometria. Ele percebeu que, ao atribuir pares de números a pontos no plano, poderia criar um sistema que permitisse representar geometricamente esses pontos e suas relações de maneira organizada.
A origem histórica do plano cartesiano remonta ao livro “La Géométrie”, publicado por Descartes em 1637. Nessa obra, ele introduziu a ideia de usar duas linhas perpendiculares (um eixo horizontal e um eixo vertical) para criar um sistema de coordenadas no qual cada ponto do plano seria representado por um par ordenado de números, conhecidos como coordenadas cartesianas.
As linhas horizontais e verticais do plano cartesiano são chamadas de eixos x (abscissas) e y (ordenadas), respectivamente. O ponto onde esses dois eixos se encontram é chamado de origem, representado pelo par ordenado (0,0). A partir da origem, os pontos são localizados em relação à distância ao longo dos eixos x e y.
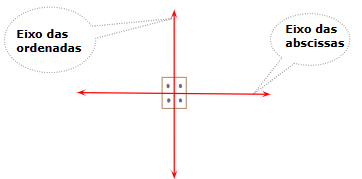
Imagem do arquivo pessoal
Transformações geométricas
As transformações geométricas no plano cartesiano são usadas para compreender a relação entre as coordenadas de pontos e figuras geométricas. Uma das operações é a multiplicação das coordenadas dos vértices de um polígono por um número inteiro, que pode resultar em uma variedade de efeitos visuais.
Quando multiplicamos as coordenadas de um ponto por um número inteiro, estamos ampliando ou reduzindo sua distância em relação à origem. Por exemplo, se multiplicarmos as coordenadas por 2, o ponto será deslocado para uma posição duas vezes mais distante da origem ao longo de cada eixo. Veja:
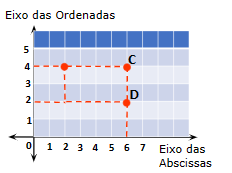
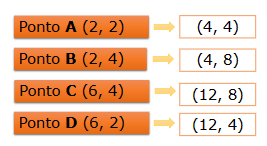
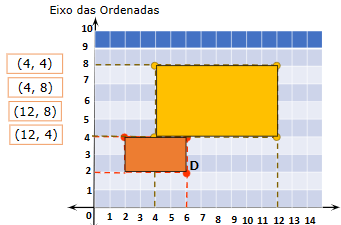
Imagens do arquivo pessoal
Simetria de Reflexão
A simetria de reflexão ocorre quando uma figura é refletida em relação a um eixo, resultando em uma imagem espelhada. Essa reflexão preserva as distâncias e os ângulos entre os pontos da figura original e sua imagem refletida. Por exemplo, ao refletir um triângulo em relação a um eixo vertical, os pontos do triângulo original são mapeados em pontos correspondentes na imagem refletida, mantendo a mesma forma e tamanho.

Disponível em: <https://www.canva.com/design/DAF_gnPjsYY/vTem8qEIWZw5uo9oeuW4CA/edit?utm_content=DAF_gnPjsYY&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> Acesso em 02 de abril de 2024.
Eixo de Simetria: Um eixo de simetria, também conhecido como eixo de reflexão, é uma linha imaginária ao longo da qual uma figura pode ser dividida em duas metades exatamente refletidas. Quando uma figura possui um eixo de simetria, cada ponto da metade de um lado da linha tem um ponto correspondente na outra metade, refletido através do eixo. Por exemplo, um círculo possui infinitos eixos de simetria, passando pelo seu centro, pois qualquer linha que passa pelo centro divide o círculo em duas metades simétricas.

Disponível em: <https://www.canva.com/design/DAF_gnPjsYY/vTem8qEIWZw5uo9oeuW4CA/edit?utm_content=DAF_gnPjsYY&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> Acesso em 02 de abril de 2024.
Para identificar se uma figura possui simetria de reflexão e encontrar seus eixos de simetria, é útil visualizar a figura e imaginar linhas de reflexão ao longo das quais a figura pode ser dividida em metades simétricas. A figura a seguir possui 8 eixos de simetria:
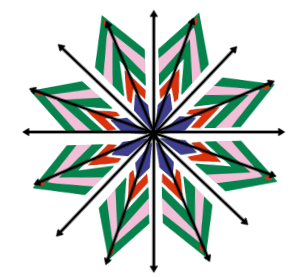
Disponível em: <https://www.canva.com/design/DAF_gnPjsYY/vTem8qEIWZw5uo9oeuW4CA/edit?utm_content=DAF_gnPjsYY&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> Acesso em 02 de abril de 2024.
Assista a videoaula com a professora Priscilla com essa temática
Vamos responder algumas questões?
Questão 1
Desenhe um plano cartesiano e marque os seguintes pontos:
- Ponto A: Abscissa 3 e ordenada 3
- Ponto B: Abscissa 3 e ordenada 6
- Ponto C: Abscissa 8 e ordenada 3
- Ponto A: Abscissa 8 e ordenada 6
Agora junte os pontos A, B, C e D e pinte a figura formada.
Questão 2
Desenhe um plano cartesiano e nele faça uma figura simétrica à figura da questão anterior com relação ao eixo das abscissas.
Questão 3
A placa de trânsito a seguir tem o formato de triângulo equilátero. Podemos afirmar que esse triângulo tem

Disponível em: <https://www.canva.com/design/DAF_gnPjsYY/vTem8qEIWZw5uo9oeuW4CA/edit?utm_content=DAF_gnPjsYY&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> Acesso em 02 de abril de 2024.
(A) um eixo de simetria.
(B) dois eixos de simetria.
(C) três eixos de simetria.
(D) nenhum eixo de simetria.
Questão 4
Ao multiplicar as coordenadas dos vértices de um polígono por um número inteiro no plano cartesiano podemos afirmar que
(A) os vértices do polígono são deslocados para posições diferentes.
(B) o polígono é girado em torno da origem.
(C) o tamanho do polígono é reduzido pela metade.
(D) o polígono é esticado ao longo do eixo x.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA19) Realizar transformações de polígonos representados no plano cartesiano, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro. (EF07MA20) Reconhecer e representar, no plano cartesiano, o simétrico de figuras em relação aos eixos e à origem. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |
