Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 8º ano do Ensino Fundamental.

Disponível em: <Fundo Mosaico Padronizar – Foto gratuita no Pixabay> Acesso em 17, maio 22.
As figuras planas que são formadas por segmentos de reta são chamadas de polígonos. A palavra POLÍGONO deriva do grego e quer dizer muitos (poly) e ângulos (gon). Nomeamos os polígonos de acordo com a quantidade de lados que possuem: um polígono de 3 lados é chamado de triângulo. O que tem 4 lados é nomeado de quadrilátero. Com 5 lados será o pentágono e assim por diante.
Os polígonos são usados em diversas áreas, como na engenharia, na arquitetura, no design gráfico e até no desenvolvimento de jogos. Ele podem ser vistos em objetos, estruturas na engenharia e até na natureza.
As colmeias das abelhas, por exemplo, são formadas por vários hexágonos.
Disponível em: < Cerveja Querida Inseto – Foto gratuita no Pixabay > Acesso em 13, maio 22
Triângulos:
Os triângulos tem 3 lados e também tem 3 ângulos internos. São figuras consideradas fundamentais na geometria. Por ser uma figura considerada indeformável é muito usado nas estruturas de grandes e pequenas construções.

No triângulo ABC representado pela figura acima, os pontos A, B e C são chamados de vértices. Os lados podem ser nomeados como AB, AC e BC. E os ângulos internos são os ângulos A, B e C. Os triângulos podem ser classificados de acordo com as medidas dos lados e de acordo com as medidas dos ângulos.
Triângulo equilátero: Possui 3 lados com a mesma medida e os 3 ângulos internos com medida igual a 60°.
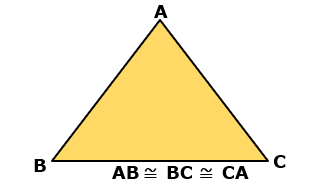
Triângulo isósceles: Possui 2 lados e 2 ângulos internos congruentes.
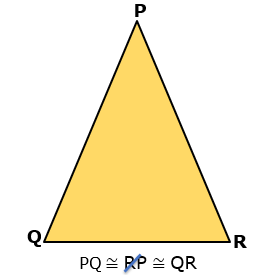
Triângulo escaleno: Tem os 3 lados e os 3 ângulos internos de medidas diferentes.
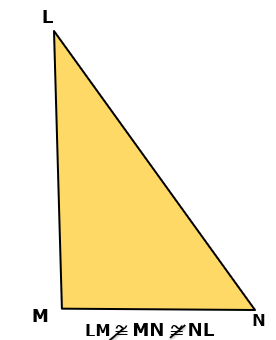
Triângulo acutângulo: Possui os 3 ângulos internos agudos. (Medida menor do que 90°)
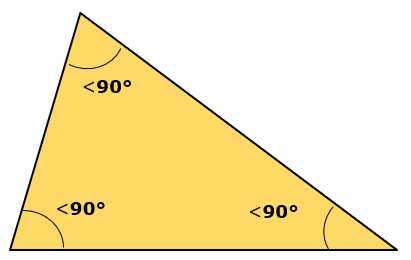
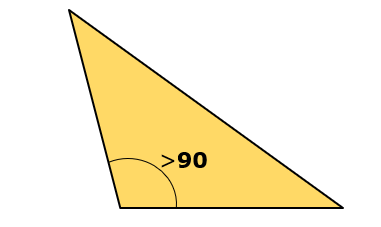
Triângulo obtusângulo: Tem um ângulo interno obtuso e os outros 2 ângulos agudos.
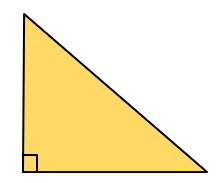
Triângulo retângulo: Possui um dos ângulos internos com medida de 90°.
Assista a videoaula abaixo da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
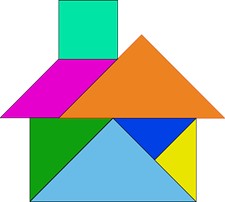
O tangram é um quebra-cabeça chinês construído com 7 peças: um quadrado, dois triângulos grandes, um triângulo médio, dois triângulos pequenos e um paralelogramo. Com ele podem ser construídas diversas formas:
Disponível em: < co vetorial grátis no Pixabay > Acesso em: 01 de agosto de 2022
Responda:
a. Quantos triângulos aparecem no tangram?
b. Qual é a classificação desses triângulos quanto aos lados?
c. Qual é a classificação desses triângulos quanto aos ângulos?
Questão 2
Durante uma aula de matemática, a professora pediu que os alunos trouxessem um exemplo de triângulo retângulo que também fosse isósceles. João desenhou um triângulo onde o ângulo A mede 90°, o ângulo B mede 45° e o ângulo C mede 45°. João classificou corretamente o triângulo? Justifique sua resposta.
Questão 3
Ana está construindo um telhado para sua casa e vai usar três pedaços de madeira que ela já tinha, para formar um triângulo. Ela mediu os lados e obteve as seguintes medidas: lado AB = 6 cm, lado BC = 6 cm e lado AC = 8 cm. De acordo com essas informações podemos afirmar que:
(A) O triângulo formado é equilátero e obtusângulo.
(B) O triângulo formado é escaleno e retângulo.
(C) O triângulo formado é equilátero e acutângulo.
(D) O triângulo formado é isósceles e acutângulo.
Questão 4
Os lados iguais de um triângulo isósceles medem 12 cm. Sabendo que o perímetro desse triângulo é igual a 43 cm, o terceiro lado mede:
(A) 24 cm
(B) 19 cm
(C) 36 cm
(D) 18 cm
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA18-A) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, tanto em suas representações no plano quanto em faces de poliedros. (EF06MA18-B) Classificar polígonos, considerando lados, vértices e ângulos em regulares e não regulares, tanto em suas representações no plano quanto em faces de poliedros. (EF07MA27) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos. (EF07MA28) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular (como quadrado e triângulo equilátero), conhecida a medida de seu lado. (EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares. (EF08MA16-B) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadro, compasso, régua e outros instrumentos |

