Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 7º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAF0WAXQIv4/oFAyc9eL58A0IwXYUq2XwA/edit?utm_content=DAF0WAXQIv4&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 16 de nov. de 2023.
A reta numérica é uma ferramenta visual que nos auxilia a compreender a organização e a relação entre diferentes números. Para localizar números racionais na reta numérica, é crucial entender a representação fracionária e decimal desses números.
Lembre-se que os números racionais são aqueles que podem ser representados na forma fracionária onde o numerador é sempre um número inteiro e o denominador é um número inteiro diferente de zero.
Representação Fracionária:
Considere a fração 3/4. O numerador (3) representa a parte que estamos considerando, e o denominador (4) indica em quantas partes iguais a unidade foi dividida. Para localizar na reta numérica, dividimos o segmento entre 0 e 1 em quatro partes iguais e marcamos três dessas partes.
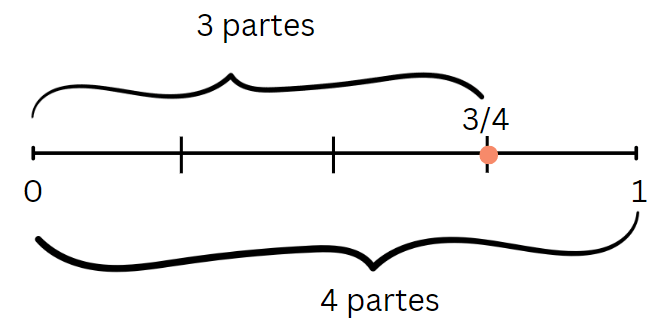
Representação Decimal:
A representação decimal é outra forma comum de expressar números racionais. A fração 3/4 pode ser escrita como 0,75 em sua forma decimal. O algarismo à esquerda da vírgula representa a parte inteira, e os algarismos à direita indicam as partes fracionárias. Na reta numérica, localizamos 0,75 entre 0 e 1, dividindo o segmento em cem partes e marcando 75 dessas partes.

Comparação de Números Racionais:
A reta numérica facilita a comparação de números racionais. Se desejarmos comparar 2/3 e 5/6, podemos colocá-los na reta numérica. Dividimos a unidade em três partes e marcamos duas para 2/3. Da mesma forma, dividimos em 6 partes e marcamos cinco para 5/6.
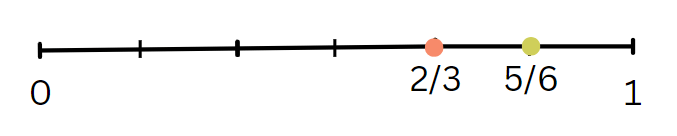
Agora, podemos visualizar que 5/6 está mais à direita, indicando que é maior que 2/3.
Dízimas periódicas:
Alguns números racionais têm representações decimais periódicas, como 0,333… Podemos escrever esse número na forma fracionária para facilitar a marcação na reta numérica: 0,3333… = 3/9 = 1/3
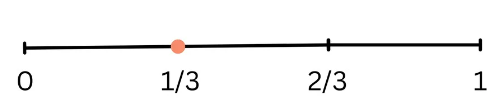
Podemos concluir que, a reta numérica é importante para visualizar e compreender números racionais. A representação fracionária e decimal nos permite localizar esses números, facilitando a comparação e a compreensão de suas relações. Ao explorar a reta numérica, desenvolvemos uma compreensão mais profunda da estrutura dos números racionais e sua distribuição ao longo da reta numérica.
Agora que você , que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Miguel está fazendo panquecas e precisa de 3/4 de xícara de leite e 1/2 xícara de farinha. A representação na reta numérica da quantidade de leite que ele usará se encontra entre os números inteiros
(A) 0 e 1
(B) 1 e 2
(C) 2 e 3
(D) 3 e 4
QUESTÃO 2
Ana, durante a semana, se compromete a estudar 1/2 hora de matemática e 3/4 hora de ciências por dia. Representando o tempo de estudo diário na reta numérica, podemos concluir que a matéria que Ana estuda por mais tempo é
(A) Português
(B) Matemática
(C) Ciências
(D) História
QUESTÃO 3
Maria está no supermercado e deseja comprar 1/2 kg de maçãs e 3/4 kg de uvas. Represente esses pesos na reta numérica e indique qual quantidade é maior.
QUESTÃO 4
João, ao seguir uma receita para fazer um bolo, precisa de 2/3 de xícara de açúcar e 1/4 de xícara de farinha. Represente essas quantidades na reta numérica e determine qual ingrediente é utilizado em maior quantidade.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA10) Comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |

