Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6° Ano do Ensino Fundamental – Anos Finais.

Disponível em: <Pagar Dígito Número – Imagens grátis no Pixabay – Pixabay> último acesso em 12 de março de 2023.
A leitura de números racionais na forma decimal é uma habilidade essencial no contexto matemático e no dia a dia. Ao compreender e dominar essa habilidade, somos capazes de interpretar e expressar quantidades racionais com precisão.
Ao ler um número racional na forma decimal, é importante compreender a relação entre as posições ocupadas pelos algarismos e os valores que eles representam. O sistema de numeração decimal é baseado em potências de 10, e cada posição à direita da vírgula possui um valor 10 vezes menor que a anterior.
Para iniciar a leitura de um número racional na forma decimal, primeiramente identificamos a parte inteira, que compreende os algarismos à esquerda da vírgula. Por exemplo, no número 123,45, a parte inteira é “123“. Em seguida, é necessário interpretar a parte decimal, que se encontra à direita da vírgula. No exemplo citado, a parte decimal é “45“.
Para ler a parte decimal, consideramos a relação entre as posições ocupadas pelos algarismos e seu valor. A primeira casa decimal representa décimos, a segunda casa representa centésimos, a terceira casa representa milésimos e assim por diante. No caso de 123,45, o “4” representa quatro décimos e o “5” representa cinco centésimos.
Ao fazer a leitura completa, combinamos a parte inteira e a parte decimal, utilizando a palavra “e” para representar a separação entre ambas. No exemplo mencionado, o número 123,45 pode ser lido como “cento e vinte e três inteiros e quarenta e cinco centésimos”.
Vejamos outro exemplo:
Vamos considerar o número racional 0,0076 e realizar sua leitura na forma decimal.
Para iniciar a leitura, identificamos a parte inteira, que neste caso é zero, pois não há algarismos à esquerda da vírgula. Em seguida, passamos para a parte decimal.
A primeira casa decimal à direita da vírgula representa décimos, a segunda casa representa centésimos e a terceira casa representa milésimos.
No número 0,0076, o “7” representa sete milésimos e o “6” representa seis décimos de milésimos.
Ao fazer a leitura completa, combinamos a parte inteira e a parte decimal, utilizando a palavra “e” para representar a separação entre ambas. Nesse caso, o número 0,0076 pode ser lido como “zero inteiros e sete milésimos e seis décimos de milésimos”.
Dominar a leitura de números racionais na forma decimal é fundamental para interpretar informações quantitativas em diferentes contextos, como nas ciências, economia, estatística e até mesmo em situações cotidianas, como lidar com dinheiro, medidas e porcentagens.
Reta numérica:
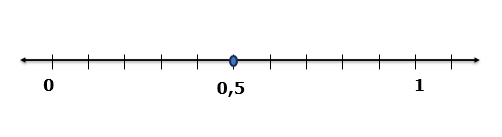
Marcar um número racional na forma decimal na reta numérica pode ser feito de forma simples e visual. Vamos considerar o número racional 0,5 como exemplo.
- Comece desenhando uma linha reta horizontal, que será a sua reta numérica.
- Marque um ponto inicial na linha e atribua a ele o valor zero.
- Identifique uma unidade de medida adequada para a sua reta numérica, por exemplo, 1 centímetro representa 0,1 na reta numérica.
- A partir do ponto zero, avance 5 unidades de medida na direção positiva da reta numérica.
- Marque um ponto nessa posição correspondente a 0,5.
Agora você tem o número 0,5 representado na reta numérica. Visualmente, você pode observar que ele está localizado entre o zero e o número 1, e é exatamente no meio do caminho entre esses dois pontos.
Ordenação de números racionais na forma decimal:
Para ordenar números racionais na forma decimal, siga os seguintes passos:
- Comece comparando as partes inteiras dos números. Coloque os números em ordem crescente ou decrescente com base em suas partes inteiras. Se as partes inteiras forem iguais, passe para a próxima etapa.
- Em seguida, compare as partes decimais dos números. Comece comparando a casa decimal mais à esquerda. Coloque os números em ordem crescente ou decrescente com base nessa casa decimal. Se as casas decimais forem iguais, passe para a próxima casa decimal. Continue comparando e ordenando as casas decimais até que todos os números estejam em ordem.
- Se alguns dos números tiverem casas decimais adicionais, mas outros não, considere que os números sem casas decimais são equivalentes a ter casas decimais zero. Por exemplo, 2,5 é o mesmo que 2,500.
- Continue comparando e ordenando as casas decimais até que todos os números estejam em ordem completa, levando em conta todas as casas decimais.
- Utilize os símbolos de maior que (>), menor que (<) ou igual a (=) para indicar a relação de ordem entre os números. Por exemplo, se tivermos os números 2,35; 2,56 e 2,14, podemos compará-los da seguinte forma: 2,14 < 2,35 < 2,56.
- Se alguns dos números tiverem casas decimais adicionais, mas outros não, considere que os números sem casas decimais são equivalentes a ter casas decimais zero. Por exemplo, 2,5 é o mesmo que 2,500.
- Continue comparando e ordenando as casas decimais até que todos os números estejam em ordem completa, levando em conta todas as casas decimais.
- Utilize os símbolos de maior que (>), menor que (<) ou igual a (=) para indicar a relação de ordem entre os números. Por exemplo, se tivermos os números 2,35; 2,56 e 2,14, podemos compará-los da seguinte forma: 2,14 < 2,35 < 2,56.
Ao ordenar números racionais na forma decimal, é importante observar tanto as partes inteiras quanto as partes decimais dos números. Essa análise cuidadosa permite que você estabeleça uma sequência precisa e correta dos números em relação às suas magnitudes decimais. Lembre-se de realizar as comparações em cada casa decimal, levando em consideração os valores numéricos presentes.
Agora que você estudou sobre leitura, escrita e ordenação de números racionais em sua representação decimal, que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Lucas está medindo a temperatura em diferentes momentos do dia e registrou as seguintes leituras: 17,3°C, 12,45°C, 18,02°C e 9,8°C. Escreva os números em ordem crescente, do menor para o maior e os represente em uma reta numérica.
QUESTÃO 2
Na fábrica de brinquedos, foram produzidos pacotes de figurinhas com as medidas de 5,25 por 7,4. A leitura correta desses números é
(A) cinco inteiros e vinte e cinco centésimos; sete inteiros e quatro décimos.
(B) cinco inteiros e vinte e cinco centésimos; sete inteiros e quarenta centésimos.
(C) cinco inteiros e vinte e cinco milésimos; sete inteiros e quatro décimos.
(D) cinco inteiros e vinte e cinco milésimos; sete inteiros e quarenta centésimos.
QUESTÃO 3
Ana está fazendo compras em uma papelaria e registrou os preços de alguns produtos: R$ 5,35; R$ 7,99; R$ 3,15 e R$ 6,50. Escreva os preços em ordem crescente, do menor para o maior, e represente-os em uma reta numérica
QUESTÃO 4
Um corredor está treinando para uma competição de corrida e cronometrou seus tempos em diferentes trechos da pista. Os tempos registrados foram: 12,75 segundos; 12,32 segundos; 12,5 segundos e 12,7 segundos. Desses tempos o menor é
(A) 12,75.
(B) 12,32.
(C) 12,5.
(D) 12,7.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA02-G) Ler, escrever e ordenar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal, utilizando, como recursos, a composição e decomposição e a reta numérica. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |

