Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 6º ano do Ensino Fundamental.
Disponível em: <Escalas De Justiça Pesar – Foto gratuita no Pixabay> Acesso em 05 de outubro de 2022.
A matemática é como um grande quebra-cabeça, cheio de peças que se encaixam de maneira surpreendente para resolver problemas e desvendar mistérios do nosso cotidiano. Vamos explorar uma dessas peças fundamentais: a propriedade de igualdade matemática. Podemos começar a compreender como essa propriedade funciona em situações simples e familiares.
Ao entendermos como as quantidades se relacionam umas com as outras, seremos capazes de resolver problemas de maneira mais inteligente e eficaz. Vamos explorar juntos essa fascinante propriedade e descobrir como ela pode nos ajudar a desvendar os segredos dos números.
Chamamos de igualdade quando duas operações ou quantidades são iguais entre si. Usamos o símbolo = para representar essa relação. As igualdades podem ser usadas para encontrar valores desconhecidos e para resolver problemas matemáticos.
Imagine que temos uma balança em equilíbrio com dois conjuntos de blocos. Em um dos lados da balança, temos um conjunto de blocos vermelhos, e no outro, um conjunto de blocos azuis. Agora, se adicionarmos um mesmo número de blocos vermelhos e azuis em ambos os lados da balança, ela permanecerá equilibrada.
Isso nos mostra que ao adicionar a mesma quantidade em ambos os lados, a relação de igualdade é preservada, mantendo a balança equilibrada.
A mesma ideia se aplica à subtração. Se removermos a mesma quantidade de blocos vermelhos e azuis de ambos os lados da balança, ela continuará equilibrada.
Além disso, se multiplicarmos ou dividirmos a quantidade de blocos de ambos os lados da balança pelo mesmo número, a relação de igualdade também será mantida. Por exemplo, se multiplicarmos todos os blocos por 2, a balança permanecerá equilibrada, desde que façamos isso em ambos os lados.
Essa propriedade é útil não apenas para balanças, mas também em muitas situações do nosso dia a dia. Por exemplo, ao dividir um bolo igualmente entre amigos, se cortarmos cada pedaço pela metade, a quantidade total de bolo permanece a mesma.
Portanto, ao entender essa propriedade de igualdade matemática, podemos resolver problemas de maneira mais eficaz e compreender melhor as relações entre diferentes quantidades. Esses conceitos fundamentais nos ajudam a desenvolver habilidades importantes para lidar com situações do mundo real de maneira mais inteligente e confiante.
Assista a videoaula da professora Priscilla com essa temática
Questão 1
Verifique se cada uma das igualdades abaixo é verdadeira:
- 2 x (5 + 4) = 2 x 5 + 4
- (15 + 25) x 2 = 2 x 22 + 36
- 12 : 4 – 1 = 3 – 2
- 34 : 2 – (4 + 3) = (12 + 8) : 2
Questão 2
Usando as propriedades da igualdade podemos concluir que o valor desconhecido é

Imagem do arquivo pessoal
(A) 10
(B) 11
(C) 12
(D) 13
Questão 3
Sabendo que figuras iguais têm o mesmo valor, calcule o valor de cada uma delas.
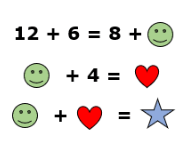
Imagem do arquivo pessoal
Questão 4
Na igualdade abaixo podemos concluir que a figura sol representa o número

(A) 10
(B) 11
(C) 12
(D) 13
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA14) Reconhecer que a relação de igualdade matemática não se altera ao adicionar, subtrair, multiplicar ou dividir os seus dois membros por um mesmo número e utilizar essa noção para determinar valores desconhecidos na resolução de problemas. (GO-EF06MA15-B) Ler, interpretar, resolver e elaborar problemas que envolvam a partilha de uma quantidade em duas partes desiguais, envolvendo relações aditivas e multiplicativas, bem como a razão entre as partes e entre uma das partes e o todo, em contextos significativos, inclusive utilizando materiais manipuláveis. |

