Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 8º ano do Ensino Fundamental.
Disponível em: <Quebra-Cabeça Matemática Lógica – Gráfico vetorial grátis no Pixabay> Acesso em 15 de outubro de 2022.
As equações do 1º grau são expressões matemáticas que envolvem uma ou mais incógnitas (ou variáveis) elevadas à primeira potência, acompanhadas por constantes (números) e operações matemáticas, tais como adição, subtração, multiplicação e divisão. Elas têm muitas aplicações no dia a dia e em diversas áreas, desde a física, engenharia e a economia.
Elas são usadas na resolução de problemas de tempo, distância e velocidade, no cálculo de descontos e acréscimos em compras, na determinação de taxas de juros em empréstimos e investimentos, e até mesmo na elaboração de receitas de culinária.
Por exemplo, ao calcular a quantidade de ingredientes necessários para uma receita, podemos utilizar uma equação do 1º grau para determinar o número de porções a serem feitas com base na quantidade de cada ingrediente disponível e na proporção indicada na receita.
Na engenharia, as equações são utilizadas para modelar e resolver problemas relacionados a circuitos elétricos, estruturas e sistemas mecânicos. Na economia, são empregadas para analisar e prever o comportamento de variáveis como oferta, demanda e preços de mercado.
Definição: Uma equação do 1º grau possui a seguinte forma geral: ax + b = 0, onde a e b são constantes conhecidas, x é a incógnita e o expoente de x é 1. O objetivo é encontrar o valor de x que torna a equação verdadeira, ou seja, que satisfaz a igualdade.
A resolução de equações do 1º grau envolve a aplicação de diferentes operações matemáticas para isolar a incógnita e determinar seu valor. O processo consiste em simplificar a equação por meio de operações algébricas até que se chegue a uma solução única para x.
Por exemplo, considere a equação 2x−4=0. Para resolver essa equação, podemos adicionar 4 aos dois lados da equação para isolar o termo 2x, obtendo 2x=4. Em seguida, dividimos ambos os lados por 2 para encontrar o valor de x, resultando em x=2. Portanto, x=2 é a solução para a equação 2x−4=0.
Veja outro exemplo de resolução de equação:
5 (2x + 3) = 2 (4x − 1) + 7
1°) Vamos começar usando a propriedade distributiva:
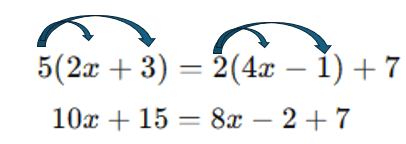
2°) Em seguida, juntamos os termos semelhantes usando as operações inversas:
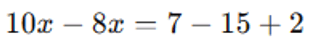
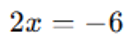
3°) Dividimos ambos os lados da equação por 10 para isolar x:
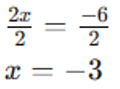
Assista a videoaula abaixo da professora Priscilla com essa temática.
Questão 1
A soma das idades de Paulo e Ana é 32 anos. A idade de Ana é 17 anos. Usando a letra “x” para representar a idade de Pedro, a equação referente a essa situação é
(A) x+17=32.
(B) x−17=32.
(C) x+17=49.
(D) x−17=49.
Questão 2
Aline fez um percurso de bicicleta de 12 km dividido em 2 trechos. No primeiro trecho ela percorreu alguns quilômetros e no outro percorreu o dobro do que havia percorrido no trecho anterior. Resolvendo essa situação usando uma equação podemos concluir que em cada trecho ela percorreu
(A) 3 km e 6 km.
(B) 4 km e 8 km.
(C) 5 km e 10 km.
(D) 6 km e 12 km.
Questão 3
Resolva usando uma equação do 1° grau: Se Maria tem o dobro da idade de sua irmã mais nova, e a soma de suas idades é 30 anos, quantos anos cada uma tem?
Questão 4
Resolva usando uma equação do 1° grau: Se um vendedor recebe um salário fixo mais uma comissão de 5% sobre o valor total das vendas, e no último mês ele recebeu R$ 1500,00, qual foi o valor total das suas vendas?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA18-A) Ler, interpretar, resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, como determinar qual a quantidade de produtos deve ser produzida para se obter determinado lucro ou receita, determinar qual a quantidade de quilômetros deve ser percorridos por um táxi para corresponder a um determinado valor de corrida. (EF07MA18-B) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à forma ax + b = c, fazendo uso das propriedades da igualdade, em situações diversas. (EF08MA07) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |