Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 8º ano do Ensino Fundamental.
Disponível em: <Quebra-Cabeça Matemática Lógica – Gráfico vetorial grátis no Pixabay> Acesso em 15 de outubro de 2022.
Introdução
Podemos observar círculos e circunferências em diversos objetos do nosso cotidiano, como pneus, anéis, pizza, entre outros. Mas, o que exatamente são círculos e circunferências? Qual a diferença entre eles? Vamos explorar essas formas geométricas e entender seus conceitos fundamentais.
Diferença entre Círculo e Circunferência
A circunferência é a linha curva formada por todos os pontos equidistantes ao ponto central de um espaço vazio delimitado por ela. Em termos mais simples, é o contorno ou a borda de um círculo.
Já o círculo inclui a circunferência e toda a superfície interna totalmente preenchida. É a área delimitada pela circunferência.
Para ilustrar, imagine uma pizza. A borda da pizza representa a circunferência, enquanto a pizza inteira, incluindo a parte coberta por queijo e ingredientes, representa o círculo.
Conceitos de Raio e Diâmetro
Dois conceitos fundamentais para entender círculos e circunferências são o raio e o diâmetro:
- Raio (r): É a distância do ponto central até qualquer ponto da circunferência. Todos os raios de um círculo são iguais.
- Diâmetro (d): É a distância entre dois pontos opostos da circunferência, passando pelo ponto central. O diâmetro é duas vezes o raio (d = 2r).
Comprimento da Circunferência
O comprimento de uma circunferência é a medida ao redor da borda do círculo. A fórmula para calcular o comprimento da circunferência é:
C = 2 . π . r
onde π (pi) é aproximadamente 3,14.
Exemplo 1: Calcular o comprimento de uma circunferência em que o raio mede 5 cm. O comprimento da circunferência é calculado como:
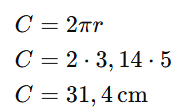
Portanto, o comprimento da circunferência é 31,4 cm.
Área do Círculo
A área de um círculo é a medida da superfície interna preenchida. A fórmula para calcular a área de um círculo é:
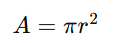
Exemplo 2: Calcular a área de um círculo cujo raio mede 7 cm:
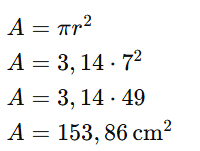
Portanto, a área do círculo é 153,86 cm².
Importância no Cotidiano
Os conceitos de círculo e circunferência são importantes em outras áreas do conhecimento:
- Engenharia e Arquitetura: Na construção de estruturas circulares como cúpulas e torres.
- Design e Arte: Na criação de objetos e obras de arte com formas circulares.
- Rodas e Engrenagens: No design de rodas, engrenagens e outras peças mecânicas.
- Ciências Naturais: Na astronomia, onde órbitas planetárias são modeladas como circunferências.
- Medicina: Em equipamentos médicos que possuem componentes circulares.
Exercícios Resolvidos
1) Dado um raio de 10 cm, encontre o diâmetro do círculo.
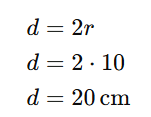
O diâmetro do círculo é 20 cm.
2) Dado o comprimento de uma circunferência de 50,24 cm, encontre o raio do círculo.
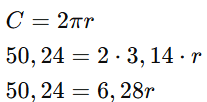
O raio do círculo é aproximadamente 8 cm.
3) Uma pizza tem um raio de 12 cm. Calcule a área da pizza.
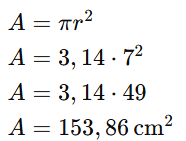
A área da pizza é 452,16 cm².
Assista a videoaula abaixo da professora Priscilla com essa temática.
Questão 1
Uma pizzaria vende dois tamanhos de pizza. A menor tem o raio igual a 15 cm e a maior tem o raio igual a 20 cm. Qual é a diferença entre as áreas dessas pizzas?
Questão 2
Ana tem um anel circular com um diâmetro de 18 mm. O comprimento da circunferência do anel é aproximadamente
(A) 56,52 mm.
(B) 28,26 mm.
(C) 36 mm.
(D) 72 mm.
Questão 3
Um jardim circular tem um raio de 5 metros. A área do jardim é, aproximadamente
(A) 25 m² .
(B) 78,5 m² .
(C) 50 m² .
(D) 157 m².
Questão 4
Mariana vai fazer guirlandas de Natal usando festão. Ela pretende fazê-las com 50 cm de diâmetro. Responda:
A) Quantos centímetros de festão ela precisará para fazer uma guirlanda? (Use pi = 3,14)
B) Se ela for fazer 12 guirlandas como essa precisará de quantos metros de guirlanda?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga e Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Habilidades: | (GO-EF09MA24) Resolver situações problema envolvendo o cálculo das medidas do comprimento da circunferência e da área do círculo. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |

