Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento H (8º ano) do Ciclo da Adolescência foi veiculada na TV no dia 03/08/2021 (Quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Na aula de hoje você estudará alguns conceitos geométricos, ressaltando o estudo das retas chamadas de cevianas que podem fazer parte da estrutura do triângulo, compreendendo as medianas, bissetrizes e mediatrizes. Ao longo da atividade você perceberá o quanto essas cevianas são importantes para compreendermos alguns aspectos estruturais no triângulo!
Assista a videoaula a seguir com a temática – Cevianas no triângulo: mediana, bissetriz e mediatriz.
Para iniciar seus estudos, tomamos por base os conhecimentos sobre o triângulo. O triângulo é o menor polígono que existe, pois possui apenas três lados.

Os lados do triângulo são: AB, BC e CA.
Como o triângulo não possui diagonal, torna-se importante fazer o estudo dos outros elementos que o compõem. Neste caso, tem-se o conceito de cevianas do triângulo, que são retas que podem compor a estrutura do triângulo. Nesta aula de matemática, estudaremos as cevianas: mediana, bissetriz e mediatriz.
Mediana no triângulo e o baricentro
A mediana no triângulo é a reta que passa pelo ponto médio do triângulo e vai até o vértice oposto ao lado do triângulo. Observe:
Tomando por base o lado BC do triângulo abaixo o ponto D é o ponto médio desse segmento (lado).

Após determinar o ponto médio de BC, traça-se uma reta (mediana) que passe pelo ponto D até o vértice A (oposto ao lado BC):

A reta que passa pelo ponto D e vértice A do triângulo é a reta mediana referente ao lado BC. Do mesmo modo, podemos traçar as outras duas retas medianas referentes ao lado AB e lado CA. Observe:

Assim, tem-se as três medianas do triângulo ABC. Note que as três medianas se encontram em um ponto interno ao triângulo.
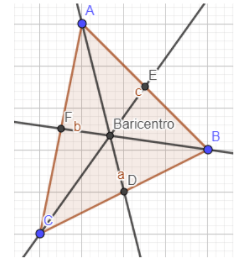
A este ponto de encontro de todas as medianas do triângulo atribuímos-lhe o nome de BARICENTRO. O baricentro é um ponto muito importante do triângulo, pois ele determina o ponto de equilíbrio do triângulo. Para verificar essa propriedade, podemos desenhar um triângulo qualquer em uma cartolina, determinar seu baricentro e em seguida cortá-lo. Se passarmos um barbante pelo baricentro, podemos suspender a representação do triângulo e deixá-lo em equilíbrio.

Você percebeu o quanto as medianas e o baricentro são importantes no triângulo? Agora, você vai estudar outra ceviana do triângulo, a bissetriz.
Bissetriz do triângulo e o incentro
A bissetriz do triângulo é esta mesma que você pensou, já estudou e provavelmente já está bem familiarizado com ela! A reta bissetriz é a reta que divide o ângulo ao meio. No triângulo é possível determinar três retas bissetrizes, uma para cada ângulo interno do triângulo.
Veja a construção da reta bissetriz com a utilização do site online https://www.geogebra.org/classic?lang=pt_PT
Dado o triângulo ABC abaixo:
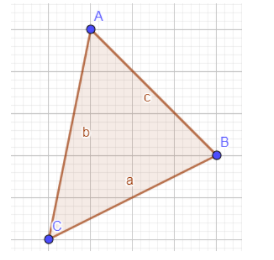
Vamos construir a reta bissetriz referente ao ângulo A.
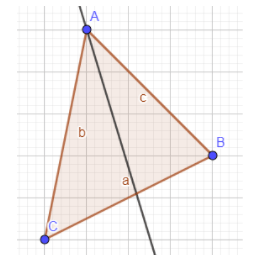
Observe que a reta bissetriz dividiu o ângulo interno A, exatamente ao meio. Do mesmo modo, agora, vamos traçar as outras duas retas bissetrizes, uma para o ângulo interno B e outra para o ângulo interno C.
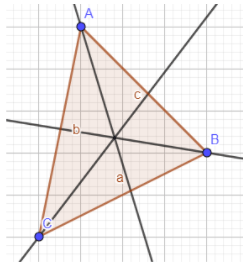
Analisando com atenção, você perceberá que, ao traçar as três retas bissetrizes do triângulo, elas se interceptam em um ponto.

A este ponto de encontro de todas as retas bissetrizes de um triângulo, atribuímos o nome de INCENTRO. O incentro é um ponto muito importante do triângulo pois ele está exatamente no centro do triângulo, sendo possível determinar uma circunferência inscrita no triângulo, ou seja, uma circunferência que está dentro do triângulo. Para isso, basta tomar como centro da circunferência o incentro e em seguida tomar como extremidade da circunferência, o lado do triângulo. Observe:

Perceba que o raio da circunferência traçada a partir do incentro mede exatamente a distância do incentro até o ponto de interceptação da bissetriz com o lado do triângulo.
Agora que você já sabe dos pontos notáveis baricentro e incentro, vamos estudar outra ceviana do triângulo, que é a mediatriz.
A reta mediatriz e o circuncentro do triângulo
A reta mediatriz do triângulo é a reta que passa pelo ponto médio do lado do triângulo e forma com o lado uma perpendicular, ou seja, é a reta que passa pelo ponto médio do lado do triângulo formando ângulos de 90º.
Observe no triângulo ABC a mediatriz referente ao lado BC.
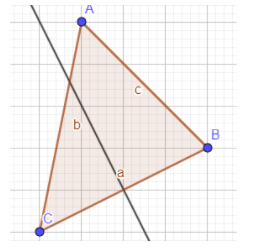
Perceba que a reta passa pelo ponto médio de BC e forma com ele ângulos de 90°.
Do mesmo modo, podemos traçar as outras duas mediatrizes do triângulo, observe:

Assim como nos casos anteriores das cevianas já estudadas, as mediatrizes do triângulo se encontram em um ponto, a este ponto, damos o nome de CIRCUNCENTRO, que é o ponto de encontro de todas as mediatrizes do triângulo.

Por meio do circuncentro é possível determinar uma circunferência circunscrita ao triângulo, ou seja, uma circunferência que intercepta todos os vértices do triângulo.
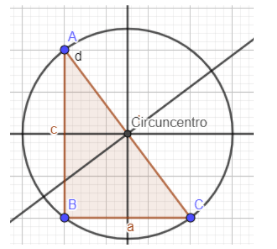
Neste caso o maior lado do triângulo retângulo recebe um nome especial, que é hipotenusa.
No entanto se o triângulo for obtusângulo o circuncentro estará fora da região delimitada pelo triângulo, observe:

Agora é com você! Coloque os seus conhecimentos em prática, resolvendo as questões a seguir.
Atividade1
Questão 01. Determine a medida do perímetro de cada triângulo, sabendo que O é o baricentro.

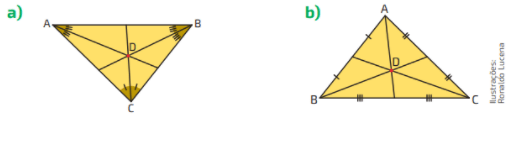
Questão 02. Uma cobertura triangular será instalada próximo de um quiosque na praia. Para isso, serão colocados quatro pontos de apoio nessa cobertura, um em cada vértice e outro em seu ponto de equilíbrio. Em qual dos esquemas os pontos A, B, C e D correspondem aos pontos de apoio da cobertura? Justifique.
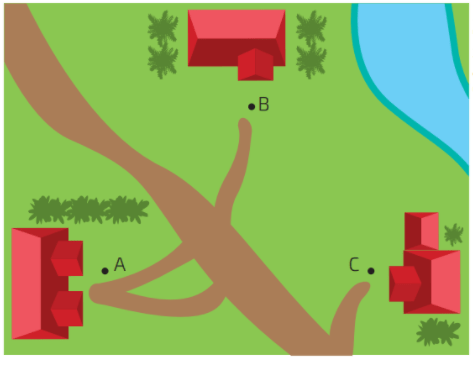
Questão 03. Em um sítio moram três famílias, que ocupam as casas indicadas no esquema por A, B e C. Pretende-se construir um poço artesiano que fique à mesma medida de distância de cada uma das casas. Em que local o poço artesiano deve ser construído?
RELEMBRANDO!
Nesta atividade de matemática, você estudou sobre as cevianas do triângulo, relembrando os elementos do triângulo e em seguida estudando as cevianas: mediana (que originam o baricentro), as bissetrizes (que originam o incentro) e as mediatrizes (que originam o circuncentro). Percebeu também, que o baricentro é o ponto de equilíbrio o triângulo, o incentro oportuniza o traçado de uma circunferência inscrita no triângulo e que o circuncentro pode determinar uma circunferência que circunscreve o triângulo. Há que se ressaltar que especialmente o circuncentro, pode estar em três lugares distintos: se o triângulo for acutângulo o circuncentro estará dentro do triângulo, se o triângulo for retângulo o circuncentro estará no ponto médio do maior lado do triângulo e se o triângulo for obtusângulo o circuncentro estará fora do triângulo.
Parabéns pelo estudo! Continue se empenhando com as atividades do conexão escola. Até a próxima atividade de matemática!
| Referências | DANTE, Luiz Roberto. Teláris matemática, 8º ano: ensino fundamental, anos finais – 3. ed. – São Paulo : Ática, 2018. PATARO, Patricia Moreno., BALESTRI, Rodrigo. Matemática essencial 8o ano : ensino fundamental, anos finais – 1. ed. – São Paulo : Scipione, 2018. PLND |
| Componente Curricular | Habilidades |
| Matemática | Estruturante (EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas. Complementares EF08MA15 EF08MA16-A EF08MA16-B |