Matemática – Resolvendo problemas com o Teorema de Tales

Esta proposta de atividade de MATEMÁTICA é destinada aos estudante do 6º Período da Educação de Jovens e Adultos–EJA

Enunciado

O Teorema de Tales afirma que:

“Quando um feixe de retas paralelas cortado por duas retas transversais, os segmentos formados, nessas transversais, são proporcionais, ou seja, a razão entre os segmentos de uma transversal é igual à razão entre os segmentos correspondentes na outra transversal”.

Na imagem abaixo, r e t são retas transversais e a, b e c são retas paralelas.

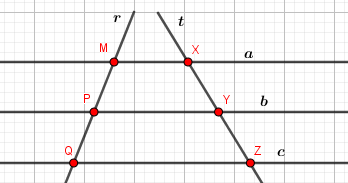
Imagem do Autor produzida no Geogebra

O Teorema de Tales afirma que os segmentos MP, PQ, XY e YZ, tomados nessa ordem, são proporcionais (mesmas razões), ou seja:

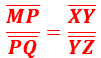
Aplicações do Teorema de Tales

O Teorema de Tales é amplamente utilizado para:

• Cálculo de medidas de segmentos.
• Cálculo da altura de prédios.
• Cálculo da altura de árvores.
• Cálculo da altura de postes e torres.

Problemas de Aplicação

Problema 1: Medidas de Segmentos

A planta abaixo, representa uma região de um determinado bairro de Goiânia. O engenheiro responsável pelo departamento de obras, quer fazer algumas reformas em calçadas e ruas, mas constatou a ausência de algumas medidas nessa planta, as quais ele representou no projeto por x e y. Com base nos dados do projeto, determinar essas medidas.

Projeto:

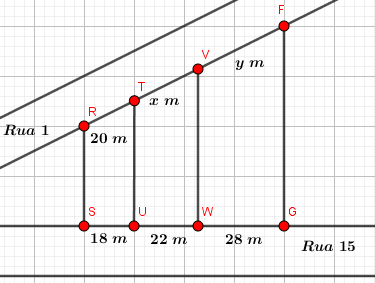
Imagem do Autor produzida no Geogebra

Resolução:

Observando na imagem, os segmentos RS, TU, VW e FG são paralelos, logo podemos afirmar, pelo Teorema de Tales, que:

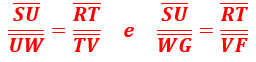
Substituindo os valores, teremos:

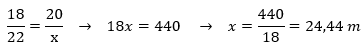
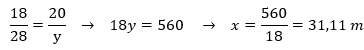
Resposta:

As medidas desconhecidas medem: x = 24,44m e y = 31,11m.

Problema 2: Altura de um Prédio

Um prédio projeta uma sombra de 20 metros no mesmo instante em que um poste de 4 metros de comprimento projeta uma sombra de 2 metros. Qual a altura do prédio?

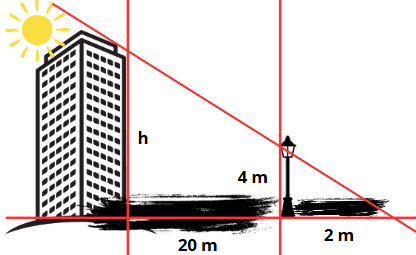
Imagem do Autor produzida no Geogebra

Resolução:

Pelo Teorema de Tales, temos a seguinte proporção:

Substituindo os valores e já resolvendo, teremos:

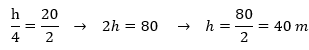
Resposta:

O prédio possui 40 metros de altura.

Ficamos por aqui, mas lembre-se que o  Teorema de Tales é uma ferramenta poderosa que nos permite resolver uma grande variedade de problemas geométricos. Sua aplicação vai além da sala de aula, sendo essencial em diversas áreas do conhecimento. Até o próximo.

Atividade

QUESTÃO 01

Na figura abaixo, a//b//c e r e t são retas transversais.

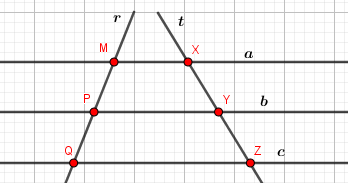
Imagem do Autor produzida no Geogebra

A) O que o Teorema de Tales afirma sobre os segmentos formados nessa figura?

B) Cite um exemplo de proporção que pode ser formada a partir dos segmentos da figura.

QUESTÃO 02

Imagine que você está construindo uma maquete de uma ponte. A ponte da maquete tem 20 cm de comprimento e a ponte real tem 100 metros. Sabendo que a altura de uma torre da ponte na maquete é de 5 cm, qual é a altura real dessa torre?

A) Qual é a proporção que podemos montar para resolver esse problema?

B) Qual é a altura real da torre?

QUESTÃO 03

Em um desenho, duas retas paralelas são cortadas por duas transversais. De acordo com o Teorema de Tales, os segmentos determinados nessas transversais são

(A) sempre iguais. 

(B) sempre diferentes. 

(C) proporcionais. 

(D) inversamente proporcionais.

QUESTÃO 04

Na figura abaixo, as retas a, b e c são paralelas e r e t transversais.

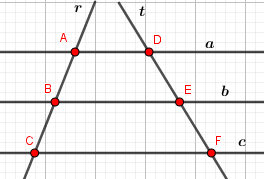
Imagem do Autor produzida no Geogebra

Se AB = 4 cm, BC = 6 cm e DE = 8 cm, podemos afirmar que o valor de EF é igual a

(A) 10 cm. 

(B) 12 cm.

(C) 14 cm.

(D) 16 cm.

Autoria	Professor Hélio Roberto da Rocha, Mestre em matemática
Componente curricular	Matemática
Objetivos de aprendizagem e desenvolvimento	(EJAMA0621) Identificar e diferenciar as razões trigonométricas fundamentais para resolver situações-problema.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024.