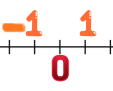Esta proposta de atividade de Matemática é destinada aos estudantes do 5º Período (6ª série) da Educação de Jovens e Adultos – EJA.
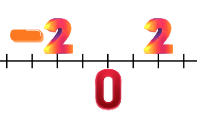
Introdução
O estudo dos números inteiros é de fundamental importância na matemática e, sua representação na reta numérica, é uma ferramenta poderosa para compreendê-los melhor.
Imagem produzida no canva/https://acesse.one/7rQQW
Neste texto, abordaremos o conceito de números inteiros, a noção de simétrico e oposto e como localizá-los na reta numérica.
Definição de Números Inteiros (Z)
Os números inteiros são números que não possuem parte fracionária, ou seja, são números inteiros positivos, negativos e o zero.
Matematicamente, denotamos os números inteiros como {…, -3, -2, -1, 0, 1, 2, 3, …}.
A letra “Z” é bastante utilizada para representar o conjunto dos números inteiros. Essa letra vem do alemão “Zahlen”, que significa “números”. Então teremos:
Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
O conjunto dos números inteiros é infinito em ambas as direções, para a esquerda e para a direita, isso significa que, a partir de qualquer número inteiro, podemos continuar contando indefinidamente para valores cada vez menores (negativos) ou maiores (positivos), sem chegar a um limite.
A reta numérica
A reta numérica é uma linha reta horizontal, cheia de pontos, onde cada ponto corresponde a um número. É infinita em ambas as direções e é dividida em segmentos de mesmo comprimento e bastante utilizada, na matemática, para comparar números e realizar operações básicas e avançadas.
Imagem do autor produzida no Geogebra
Localização dos números inteiros na Reta Numérica
Para localizar um número inteiro na reta numérica, começamos marcando o zero. Em seguida, seguimos para a direita para os números positivos e para a esquerda para os números negativos. A distância entre os números inteiros consecutivos é sempre a mesma.
Veja alguns números representados na reta numérica.
Imagem do autor produzida no Geogebra
Simétrico e Oposto
O simétrico de um número inteiro em relação à origem é o número que está à mesma distância da origem, mas no lado oposto da reta numérica.
Por exemplo:
- o simétrico de 3 é – 3, e vice-versa.
- o simétrico de – 9 é 9, e vice-versa.
Veja o simétrico de -2 na reta numérica:
Imagem do autor produzida no Geogebra
O oposto de um número inteiro é simplesmente o número que, somado a ele, resulta em zero.
Por exemplo:
- o oposto de -5 é 5, pois – 5 + 5 = 0 e
- o oposto de 2 é -2, pois 2 – 2 = 0.
Ficamos por aqui, espero que o estudo dos números inteiros na reta numérica lhe ajude a visualizar e compreender melhor os próximos assuntos a serem trabalhados com este tema.
QUESTÃO 01
Durante uma semana, a temperatura média diária em uma cidade foi de 25°C. No entanto, em um dia específico, a temperatura foi de -10°C.
A) Qual é a temperatura oposta à temperatura registrada nesse dia?
B) Qual seria a temperatura simétrica à temperatura registrada nesse dia em relação à média semanal?
C) Se a temperatura fosse -15°C, qual seria a temperatura simétrica em relação à média semanal?
QUESTÃO 02
Durante uma semana de inverno, as temperaturas médias diárias em uma cidade foram de 5°C. Em um dia específico, a temperatura foi de -3°C.
A temperatura oposta à registrada nesse dia e a temperatura simétrica em relação à média semanal são
(A) Oposta: -3°C, Simétrica: -13°C.
(B) Oposta: 3°C, Simétrica: 13°C.
(C) Oposta: -3°C, Simétrica: -5°C.
(D) Oposta: 3°C, Simétrica: -5°C.
QUESTÃO 03
Considere os números inteiros -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5.
Desenhe uma reta numérica e posicione os números inteiros de forma que o número 3 esteja a uma distância de 2 unidades do zero.
QUESTÃO 04
O número que está localizado mais próximo do zero em uma reta numérica é o
(A) -4.
(B) 3.
(C) -1.
(D) 2.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0503) Comparar e ordenar números inteiros, associá-los a pontos da reta numérica e utilizá-los em situações-problema que envolvam operações fundamentais. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 7º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 7° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. |