Esta proposta de atividade de Matemática é destinada aos estudantes do 6º Período (8ª série) da Educação de Jovens e Adultos – EJA.
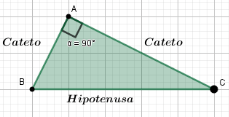
Quem é o triângulo retângulo?
O triângulo retângulo é um tipo de triângulo que possui um ângulo interno reto (90°) no qual a hipotenusa é o lado oposto ao ângulo reto (maior lado), enquanto os outros dois lados são conhecidos como catetos.
Imagem do autor produzida no Geogebra
O que são relações métricas no triângulo retângulo?
As relações métricas são fórmulas que relacionam as medidas dos comprimentos dos lados de uma figura. São, na maioria das vezes, utilizadas para resolver problemas sobre medidas de comprimentos de lados, altura e projeções de um triângulo retângulo.
Elementos de um triângulo retângulo
Considere o triângulo retângulo RST, nele destacamos alguns elementos principais que se utilizam das relações métricas para determinar suas medidas:
Imagem do autor produzida no Geogebra
- Hipotenusa (a): é o lado oposto ao ângulo reto.
- Catetos (b e c): são os dois lados que formam o ângulo reto.
- Altura (h): é a altura do triângulo retângulo RST.
- Projeções (m e n): são as projeções ortogonais dos catetos RS e RT.
Quais as principais relações métricas de um triângulo retângulo?
As principais são:
- Teorema de Pitágoras: o quadrado da hipotenusa é igual a soma dos quadrados dos catetos. ( a2 = b2 + c2 ).
- Relação altura/projeções: o quadrado da altura é igual ao produto das projeções ( h2 = m.n ).
- Relação cateto/hipotenusa/projeção: o quadrado do cateto é igual ao produto da hipotenusa pela sua projeção ortogonal (c2 = a.m e b2 = a.n)
- Relação cateto/cateto/hipotenusa/altura: o produto dos catetos é igual ao produto da hipotenusa pela altura do triângulo (b.c = a.h).
Em resumo:
a2 = b2 + c2 h2 = m.n c2 = a.m b2 = a.n b.c = a.h
Essas relações podem ser comprovadas por semelhança de triângulos, acesse o link abaixo que você poderá relembrar um pouco desse assunto.
Dois problemas para fixar esse assunto
Problema 1:
Determinar a medida da altura do triângulo retângulo PQS abaixo:
Imagem do autor produzida no Geogebra
Solução:
Aplicando a relação altura/projeções, teremos:
h2 = m.n ( Substituindo os valores: m = 4 e n = 9)
h2 = 4.9
h2 = 36 (Extraindo a raiz quadrada)
h = 6
Resposta: A medida da altura do triângulo PQS é igual a 6 unidades.
Problema 2
Determinar as medidas dos catetos do triângulo XYZ abaixo:
Imagem do autor produzida no Geogebra
Solução:
Aplicando a relação cateto/hipotenusa/projeção, teremos:
No triângulo a hipotenusa mede 14 (5+9) e as projeções medem 5 e 9, então
c2 = a.m
c2 = 14.5
c2 = 70 (Extraindo a raiz quadrada)
c ≃ 8,4
b2 = a.n
b2 = 14.9
b2 = 126 (Extraindo a raiz quadrada)
b ≃ 11,2
O símbolo ≃ quer dizer que o valor é aproximado.
Ficamos por aqui, até o próximo
Atividade
QUESTÃO 01
Em um triângulo retângulo XYZ, as projeções ortogonais dos catetos sobre a hipotenusa YZ são YH e HZ. Se a projeção YH sobre a hipotenusa mede 5 cm e a projeção HZ sobre a hipotenusa mede 8 cm, calcule a altura do triângulo a partir dessas medidas.
Imagem do autor produzida no Geogebra
QUESTÃO 02
No triângulo retângulo ABC abaixo, BC representa a hipotenusa, AB e AC são os catetos e BD e DC as projeções ortogonais dos catetos. Determinar as medidas do cateto AB (b) e da projeção DC (n).
Imagem do autor produzida no Geogebra
QUESTÃO 03
No triângulo retângulo PQR, podemos afirmar que os catetos, b e c, medem, aproximadamente
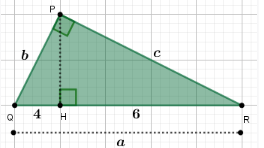
(A) 6,3 e 7,7
(B) 7,7 e 6,3
(C) 5,3 e 6,3
(D) 6,3 e 5,3
Imagem do autor produzida no Geogebra
QUESTÃO 04
No triângulo retângulo MNO, se a hipotenusa, NO, mede 24, então, podemos afirmar que a projeção m do cateto MO, mede
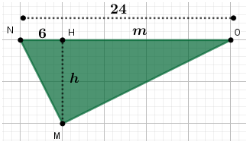
(A) 14
(B) 16
(C) 18
(D) 20
Imagem do autor produzida no Geogebra
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Objetivos de Aprendizagem e Desenvolvimento: | (EJAMA0620) Interpretar, resolver e elaborar situações-problema envolvendo relações métricas no triângulo retângulo e as relações de proporcionalidade nas retas paralelas cortadas por secantes. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. PATARO, Patricia Moreno Matemática essencial 9° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018. |

