Esta proposta de atividade de Matemática é destinada aos estudantes do 5º Período da Educação de Jovens e Adultos – EJA.

Introdução
O Máximo Divisor Comum (MDC) de dois ou mais números é o maior número que divide todos eles exatamente, sem deixar resto. Em outras palavras, é o maior divisor comum entre esses números. Neste texto iremos abordar esse assunto.
Imagem: canva.com/contas
Como determinar o MDC?
Existem diferentes métodos para determinar o MDC de dois números. Hoje, vamos apresentar somente um desses diferentes métodos, o Método da Fatoração.
Método da Fatoração
O Método da Fatoração consiste em listar os fatores primos de cada número, identificar os fatores que são comuns a ambos os números e por fim multiplicar esses fatores comuns entre si. O resultado dessa multiplicação será o MDC dos dois números.
Exemplo:
Determinar o MDC de 36 e 48.
- Listando os fatores primos de 36 e 48 (Lembre-se do MMC):
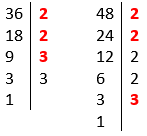
- Identificando os fatores primos que são comuns:
Fatores primos de 36: 2, 2, 3 e 3.
Fatores primos de 48: 2, 2, 2, 2, e 3.
Fatores comuns: 2, 2 e 3 (Os que estão em negrito).
- Calculando o MDC:
MDC = 2 . 2 . 3 = 12.
Aplicações do MDC
O MDC é amplamente utilizado em diversas áreas, como:
- Simplificação de Frações: para simplificar uma fração, divide-se o numerador e o denominador pelo MDC.
- Resolução de Problemas de Divisibilidade: ajuda a determinar se um número pode ser dividido por outro sem deixar resto.
- Problemas de Participação: utilizado para dividir um conjunto em partes iguais.
Exemplos de Aplicação
- Simplificação de Frações
Simplifique a fração 48/60
Calculando o MDC de 48 e 60 pelo método da fatoração, teremos:
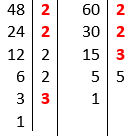
Fatores primos de 48: 2, 2, 2, 2, e 3.
Fatores primos de 60: 2, 2, 3 e 5.
Fatores comuns: 2, 2 e 3 (Os que estão em negrito).
MDC = 2 . 2 . 3 =12.
Dividindo o numerador e o denominador por 12 encontraremos a fração simplificada:
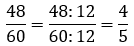
- Problema de Partição
João tem 36 laranjas e 24 maçãs. Ele quer dividir as frutas em cestas com o mesmo número de frutas em cada cesta, sem misturar os tipos de frutas. Qual é o maior número de frutas que se pode colocar em cada cesta?
Determinando o MDC de 36 e 24:
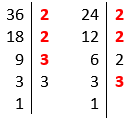
Fatores primos de 36: 2, 2, 3 e 3.
Fatores primos de 24: 2, 2, 2 e 3.
Fatores comuns: 2, 2 e 3 (Os que estão em negrito).
MDC = 2 . 2 . 3 =12.
O MDC é o maior número de frutas que pode ser colocada em cada cesta.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
O maior número natural que divide exatamente 12 e 18 é:
(A) 3.
(B) 6.
(C) 4.
(D) 9.
QUESTÃO 02
O maior divisor comum entre 15 e 35 é um número:
(A) Par.
(B) Ímpar.
(C) Múltiplo de 7.
(D) Múltiplo de 10.
QUESTÃO 03
Você tem 48 lápis e 36 canetas, e quer distribuí-los em pacotes iguais, de forma que cada pacote contenha o mesmo número de lápis e canetas. Qual é a maior quantidade de pacotes que você pode fazer?
QUESTÃO 04
Imagine que você tem 72 maçãs e 8 caixas. O objetivo é distribuir todas as maçãs pelas caixas de forma que sobre o mínimo possível de maçãs em alguma caixa. Qual é a maior quantidade de maçãs que você pode colocar em cada caixa?
SAIBA MAIS
Aprenda um pouco mais como determinar o MDC no vídeo do canal do Prof. Hélio
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0501) Resolver e elaborar situações-problemas com números naturais, envolvendo as noções de divisor e de múltiplo, incluindo os conceitos de máximo divisor comum ou mínimo múltiplo comum. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6° ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
