Esta proposta de atividade de Matemática é destinada aos estudantes do 6º Período (8ª série) da Educação de Jovens e Adultos – EJA.
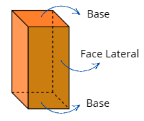
Prisma
Os prismas são figuras em 3D (tridimensionais) com duas bases iguais e paralelas, conectadas por faces retangulares ou paralelogramos.
Imagem: canva.com/prisma_https://encurtador.com.br/hiY08
Alguns exemplos práticos:
- Caixa de sapatos: as bases são retangulares e as faces laterais são retângulos.
- Lápis sextavado: as bases são hexágonos (6 lados) e as faces laterais são retângulos.
- Caixa de leite: as bases são retangulares e as faces laterais também são retângulos.
Imagem: canva.com/caixa_lápis_leite_https://encurtador.com.br/hiY08
Elementos de um prisma
Além das faces laterais e das bases, os prismas possuem os seguintes elementos:
- Arestas da base: são as arestas que formam o contorno da base do prisma.
- Arestas laterais: são as arestas que conectam as arestas correspondentes das bases.
- Vértices: são os pontos onde as arestas se encontram.
Imagem: canva.com/prisma_https://encurtador.com.br/hiY08
Como dar nome aos prismas?
Os prismas são denominados de acordo com o tipo de polígono que compõe as suas bases.
Por exemplo:
- Prisma Retangular: possui bases retangulares.
- Prisma Triangular: possui bases triangulares.
- Prisma Pentagonal: possui bases pentagonais.
- Prisma Hexagonal: possui bases hexagonais.
Imagem: canva.com/prismas_https://encurtador.com.br/hiY08
Relação entre o número de vértices, faces e arestas de um prisma
A relação entre o número de vértices (V), faces (F) e arestas (A) de um prisma é dada pela Fórmula de Euler:
V+F−A=2
Esta fórmula expressa a relação característica entre os vértices, as arestas e as faces de um prisma.
Abaixo temos uma tabela onde poderemos verificar essa relação.
Essa fórmula é útil para calcular o número de vértices, arestas e faces de qualquer prisma, desde que se conheça os valores de dois desses elementos.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
Determine:
A) O número de faces de um prisma retangular.
B) O número de arestas de um prisma pentagonal.
C) O número de vértices de um prisma hexagonal.
QUESTÃO 02
O número de arestas de um prisma triangular é igual a
(A) 3
(B) 6
(C) 9
(D) 12
QUESTÃO 03
Utilizando a relação V+F-A=2, conhecida como a Fórmula de Euler para prismas, determinar:
A) O número de faces de um prisma com 8 vértices e 12 arestas.
B) O número de vértices de um prisma que possui 10 arestas e 7 faces.
QUESTÃO 04
O número de vértices de um prisma com 10 arestas e 6 faces é igual a
(A) 8
(B) 6
(C) 10
(D) 12
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Objetivos de Aprendizagem e Desenvolvimento: | (EJAMA0622) Quantificar e estabelecer relações entre o número de vértices, faces e arestas de prismas e pirâmides, em função do polígono da base. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. PATARO, Patricia Moreno Matemática essencial 9° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018. |
