Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.

Disponível em: <Escola Estudo Aprender – Foto gratuita no Pixabay > Acesso em 30 de agosto de 2022
A matemática é uma linguagem universal que permeia diversas áreas do conhecimento, sendo essencial para compreender e interpretar fenômenos presentes no mundo que nos cerca.
Nesse sentido, as funções matemáticas desempenham um papel fundamental em diversas áreas da matemática e têm ampla aplicação em várias disciplinas científicas e práticas do mundo real.
O que é uma função?
Uma função é uma instrução matemática que associa cada valor x de um conjunto A a um único valor y de um conjunto B. Esses conjuntos são chamados de domínio e contradomínio. Além disso, x e y são designados como variável independente e variável dependente, respectivamente, uma vez que o valor de y sempre está condicionado ao valor de x.
Função de 1º Grau:
A função de 1º grau, também conhecida como função linear, é uma relação matemática entre duas variáveis, representada pela equação y = ax+b. Nessa equação, a e b são números reais, e a é diferente de zero. Esse tipo de função também recebe o nome de função afim.
As características fundamentais dessa função são sua linearidade e a representação gráfica por uma reta.
Exemplos:
y = 2x + 6
y = -x + 2
y = 0,5x
Representação gráfica da função de 1º Grau:
Para fazer a representação, devemos descobrir os pares ordenados. Para isso vamos escolher alguns valores para x (por exemplo, -2, -1, 0, 1, 2) e calcule os valores correspondentes de y usando a equação da função.
Depois dessa etapa, para cada par de valores (x , y) que calculamos, devemos marcar os pontos no plano cartesiano.
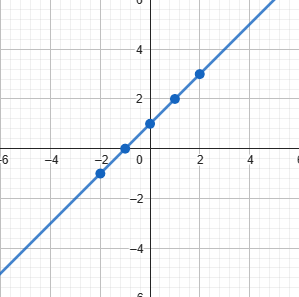
Então, vamos conectar os pontos marcados no plano cartesiano com uma linha reta. Isso representa graficamente a função linear.
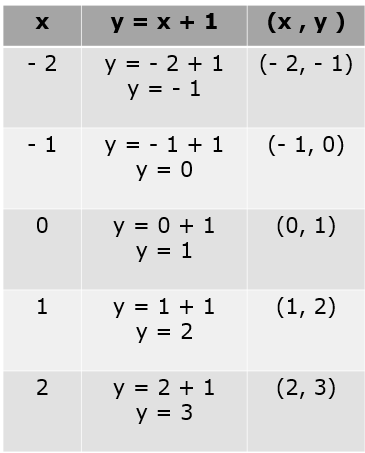
Função de 2º Grau:
Uma função quadrática é uma expressão matemática que pode ser formulada da seguinte maneira:
f(x) = ax2 + bx + c
Nesta equação, a, b e c são números reais conhecidos como coeficientes, sendo crucial que a seja sempre diferente de zero.
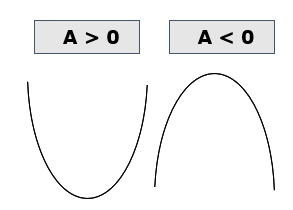
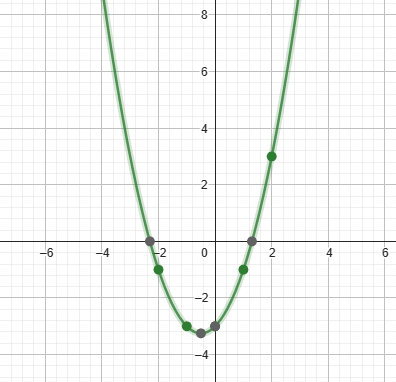
Gráfico de uma função de 2º Grau:
O gráfico de uma função de 2° grau é uma parábola com a abertura para cima se a > 0, e para baixo se a < 0.
Exemplo:
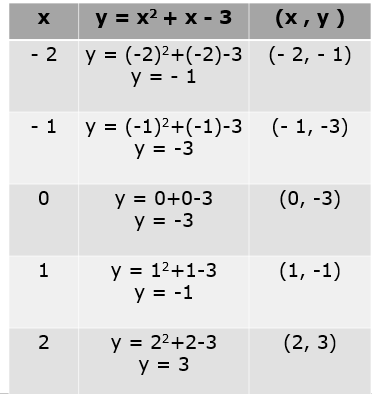
Assista a videoaula da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
Um estacionamento cobra R$5,00 pela hora inicial e 3 reais por cada hora adicional.
a) Qual o valor a ser pago por alguém que deixou o carro por 2 horas?
b) E por alguém que deixou o carro por 3 horas?
c) Represente o valor a ser pago usando uma função.
d) Faça a representação gráfica dessa função.
Questão 2
Seja a função y = f(x) = x² – 4x + 3 complete a tabela e depois faça a representação gráfica.
| x | y = x² – 4x + 3 | y |
Questão 3
Mariana comprou um pacote de mensagens de texto para seu celular. Ela pagou R$ 10 pelo pacote e mais R$ 0,50 por cada mensagem enviada. A função que modela o custo total C em relação ao número de mensagens enviadas m é dada por C(m) = 0,50m+10. O que representa o coeficiente 0,50 na função?
(A) O custo inicial do pacote de mensagens.
(B) O número total de mensagens enviadas por Mariana.
(C) A taxa de variação do custo por mensagem.
(D) O custo total pago por Mariana.
Questão 4
Lucas está economizando dinheiro para comprar um videogame. Ele começou com R$ 50 e está economizando R$ 20 por semana. A função que modela a quantia de dinheiro M em relação ao número de semanas w é dada por M(w) = 20 w + 50. O que representa o coeficiente 20 na função?
(A) A quantia inicial de dinheiro que Lucas tinha.
(B) O número de semanas que Lucas economizou.
(C) A taxa de variação da quantia de dinheiro por semana.
(D) O preço do videogame que Lucas deseja comprar.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA17-A) Ler, interpretar, resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, para calcular a quantidade de um produto ao valor a pagar, alterar as quantidades de ingredientes de receitas, ampliar ou reduzir escala em mapas, entre outros. (EF07MA17-B) Ler, interpretar, resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas. (EF08MA13) Ler, interpretar, resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas |
