Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.

Disponível em: <Matemática Fórmula Física – Imagens grátis no Pixabay> Acesso em 15 de agosto de 2022.
As equações do 2º grau e produtos notáveis são conceitos da matemática aplicados em diversas áreas do conhecimento, como física, engenharia e ciências sociais. Neste texto, abordaremos de forma detalhada esses dois temas importantes.
Equações do 2º Grau: Uma equação do 2º grau é uma equação polinomial da forma ax² + bx + c = 0, onde “a”, “b” e “c” são constantes conhecidas, e “x” é a incógnita que desejamos encontrar. O coeficiente “a” não pode ser igual a zero, pois isso resultaria em uma equação do 1º grau. A solução de uma equação do 2º grau pode ser obtida através da fórmula quadrática, que é dada por:
x = (-b ± √(b² – 4ac)) / 2a
Essa fórmula é conhecida como a fórmula de Bhaskara, em homenagem ao matemático indiano do século XII, Bhaskara Akaria. A raiz da expressão dentro da raiz quadrada, conhecida como discriminante (Δ), determina a natureza das soluções da equação.
Se Δ > 0, a equação possui duas raízes reais e distintas;
Se Δ = 0, ela possui duas raízes reais e iguais;
Se Δ < 0, não possui raízes reais, mas sim raízes complexas.
As equações do 2º grau estão presentes em problemas do cotidiano, como calcular trajetórias de objetos em lançamentos ou prever a quantidade de produtos vendidos em uma empresa.
Produtos Notáveis: Produtos notáveis são expressões algébricas que surgem com frequência em diversas situações, e são úteis para facilitar cálculos e resolver equações mais complexas. Os produtos notáveis mais comuns são:
- Quadrado de um binômio: (a + b)² = a² + 2ab + b². Esse produto é aplicado quando precisamos elevar a soma de dois termos ao quadrado.
- Quadrado da diferença de dois termos: (a – b)² = a² – 2ab + b². Esse produto é útil para simplificar expressões onde a diferença de dois termos é elevada ao quadrado.
- Produto da soma pela diferença de dois termos: (a + b)(a – b) = a² – b². Esse produto é aplicado para simplificar expressões que possuam a diferença de dois termos multiplicada pela sua soma correspondente.
- Cubo de um binômio: (a + b)³ = a³ + 3a²b + 3ab² + b³. Esse produto é utilizado quando precisamos elevar a soma de dois termos ao cubo.
- Cubo da diferença de dois termos: (a – b)³ = a³ – 3a²b + 3ab² – b³. Esse produto é aplicado quando a diferença de dois termos é elevada ao cubo.
Esses produtos notáveis facilitam a simplificação de expressões algébricas, tornando a resolução de problemas mais ágil e eficiente. Além disso, eles também são fundamentais para o estudo de limites e derivação em cálculo, desempenhando um papel crucial na matemática avançada.
Em conclusão, as equações do 2º grau e os produtos notáveis são conceitos matemáticos essenciais que desempenham um papel significativo na resolução de problemas e na compreensão de fenômenos do mundo real. Dominar esses conceitos possibilita a aplicação eficaz da matemática em diversas áreas do conhecimento.
Assista a videoaula da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
Copie no seu caderno a tabela a seguir e complete-a com os produtos notáveis:

Imagem do arquivo pessoal.
Questão 2
Bernardo estava resolvendo uma atividade de Matemática com a seguinte sentença: (2x + 3y) 2 . O resultado que ele obteve ao resolver de forma correta foi:
(A) 2x2 + 6y + 3y2
(B) 4x2 + 12y + 6y2
(C) 4x2 + 12y +9y2
(D) 2x2 + 12y + 6y2
Questão 3
Complete a resolução dos seguintes produtos notáveis:
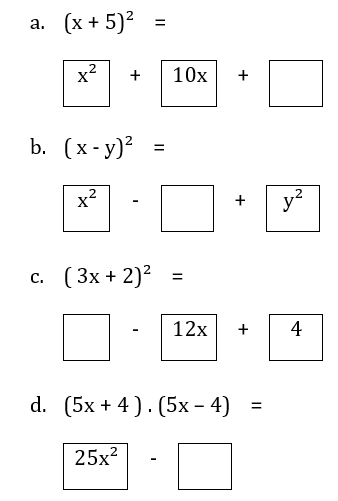
Questão 4
Qual a forma reduzida da equação que melhor representa essa situação: “A soma do quadrado de um número com o seu dobro tem como resultado 8.”
(A) x2 + 2y + 8 = 0
(B) x2 + 2y – 8 = 0
(C) 2x2 + 2y + 8 = 0
(D) x2 + 2y – 8 = 0
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA09-A) Investigar, por meio de possíveis raízes inteiras com soma S e produto P, as soluções de equações do 2° grau que podem ser comparadas à forma x² – Sx + P = 0. (EF09MA09-B) Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau, em contextos significativos. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |
