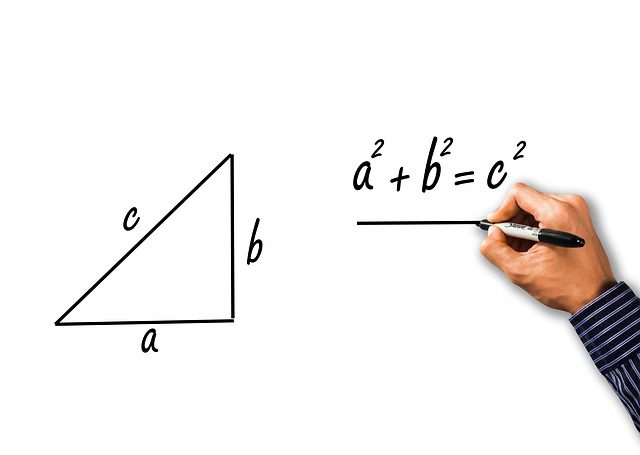Olá pessoal, hoje vamos estudar sobre o Teorema de Pitágoras;tambémiremos aprofundar em sua demonstração. Você irá aprender a forma decalcular seus catetos e hipotenusa.
Leia a seguir o texto sobre o teorema de Pitágoras e suas características:
Teorema de Pitágoras
Autores: Denise Pimpao Amaral, HenryDays
O Teorema de Pitágoras é considerado uma das principais descobertas da Matemática. Ele descreve uma relação existente no triângulo retângulo. Vale lembrar que o triângulo retângulo pode ser identificado pela existência de um ângulo reto, isto é, que mede 90º. O triângulo retângulo é formado por dois catetos e a hipotenusa, que constitui o maior segmento do triângulo e localiza-se opostamente ao ângulo reto.
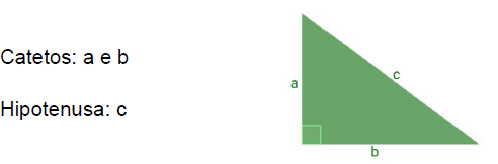
Assista ao vídeo explicativo com a demonstração do Teorema de Pitágoras no Geogebra:
Assista ao vídeo explicativo sobre como calcular o Teorema de Pitágoras:
YouTube
Baixe o aplicativo Geogebra para celular (procurar o aplicativo na Play Store) e construa um exemplo no aplicativo Geogebra, sobre o Teorema de Pitágoras e salve seu trabalho.
Para colocar seus conhecimentos em prática, resolva o seguinte exercício:
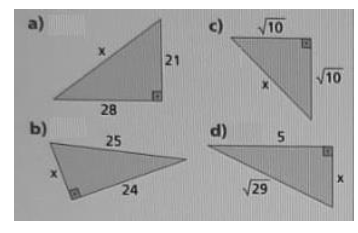
Calcule a medida x em cada um dos triângulos retângulos a seguir:
Saiba Mais | Referências:
*Vídeo GEOGEBRA: Aprendendo a Usar o programa online
(Link:https://www.youtube.com/watch?v=RMlSxruWnaA)
*Vídeo sobre como usar o Geogebra no celular
(Link: https://youtu.be/R5Vqe9Q68ZY);
*Como calcular o Teorema de Pitágoras (Link:
https://www.youtube.com/watch?v=fan2ewagFxs).
| Objeto de Conhecimento | Teorema de Pitágoras |
| Habilidades | (EF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o Teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos. |
| Proponentes/ Professores: | Professor: MárcioTadeu Mansine. |
| Instituição Educacional: | Escola Municipal Amâncio Seixo de Brito |
| CRE: | Maria Helena Bretas |
Ciclo da Adolescência – Turma I (9º ano) – Ed. Financeira e Empreendedorismo