Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8º Ano do Ensino Fundamental – Anos Finais.
Sistema de equações lineares

Algumas situações cotidianas envolvem uma relação descrita por mais de uma equação com duas incógnitas. Veja só esse exemplo.
A lanchonete do bairro anunciou as promoções dos combos da semana:
- Combo 1: 1 sanduíche e 1 refrigerante por R$18,00;
- Combo 2: 2 sanduíches e 1 refrigerante por R$28,00.
Qual é o preço do sanduíche e do refrigerante na promoção?
Os preços do sanduíche e do refrigerante não são iguais. E também não sabemos quais são. Mas, a situação narrada acima demonstra uma relação entre esses preços e o valor final do combo promocional que pode ser observada na análise da tabela abaixo.
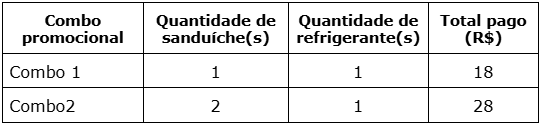
Essa relação pode ser representada por equações. Nestas equações, os valores desconhecidos podem ser substituídos por letras, ou incógnitas. Aqui usaremos:
- x = quantidade de sanduíches no combo escolhido;
- y = quantidade de refrigerante no combo escolhido.
Para cada combo vamos criar uma equação com a relação informada acima:
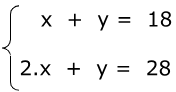
Aqui temos, portanto, um sistema de equações de 1° grau.
E o que é um sistema de equações?
É um conjunto com duas ou mais equações com mais de uma incógnita. Para que esse sistema possa ser resolvido, é preciso que a quantidade de equações seja igual ou maior que a quantidade de variáveis.
Será considerada solução do sistema, o par de números (x, y) que, ao serem substituídos nas duas equações desse sistema, tornam as operações verdadeiras.
Um sistema pode ser resolvido por diferentes estratégias. Cálculo mental, tentativa e erro (arrisca valores até encontrar a resposta correta), ou a aplicação de um dos métodos matemáticos: adição, substituição ou comparação.
Método de Adição:
Consiste em somar as duas equações de modo que uma das variáveis seja eliminada (valores opostos). Depois é só substituir na outra equação, o valor determinado para a variável.
Vejamos como funciona.

Método de Substituição:
Consiste em usar uma relação direta entre as incógnitas para solucionar o sistema. Deve-se isolar uma das variáveis em uma das equações e substituir na outra equação.

Método de Comparação:
Este método parte do princípio que a solução é única para as duas equações. Basta portanto, isolar uma mesma variável em cada uma das equações e igualar as relações encontradas.
Veja como funciona.

Que tal revisar alguns conceitos importantes para compreender as equações lineares? Então, assista a videoaula da professora Cristiane Souza, “Equações e sistemas lineares”, do Canal Estúdio Conexão Escola, no YouTube.
Agora, resolva as atividades a seguir.
QUESTÃO 1
Na barraca de doces, Pedro comprou 3 pés-de-moleque e 4 cocadas gastando R$9,50. Pedro não sabe o preço de cada produto. Mas, se considerar com x o preço unitário do pé-de-moleque e y o preço unitário da cocada, a equação que representa o gasto de Pedro é
(A) 3.x – 4.y = 9.
(B) 3.x – 4.y = 7.
(C) 4.x + 3.y = 7.
(D) 3.x + 4.y = 9.
QUESTÃO 2
A equação x – 2y = 5 é uma equação do 1º grau que possui duas incógnitas: x e y. Um par ordenado (x, y) será considerado uma solução dessa equação se, ao substituirmos os valores de x e y, a igualdade for verdadeira.
Agora faça:
A) Escolha um valor qualquer para y. Substitua esse valor em y e calcule o valor de x.
B) Se você tivesse escolhido outro valor para y, o que mudaria na sua resposta?
C) O par (9, 2) é uma solução para a equação x – 2y = 5? Justifique com cálculos a sua resposta.
QUESTÃO 3
Uma turma confeccionou 50 cartões, entre simples e decorados, que serão vendidos na festa junina da escola. Cada cartão simples será vendido por R$3,00 e o cartão decorado por R$5,00. Se todos os cartões forem vendidos, a turma arrecadará R$190,00.
A) Considerando
- x a quantidade de cartões simples e
- y a quantidade de cartões decorados,
escreva o sistema de equações que representa a situação.
B) Resolva o sistema de equações calculando os valores de x e y.
QUESTÃO 4
Seja o sistema de equações
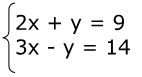
É uma solução do sistema
(A) (5, -1).
(B) (-1, 5).
(C) (5, 1).
(D) (-5, 1).
QUESTÃO 5
Dado o sistema de equações
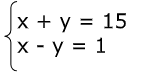
A) Como resolver esse sistema?
Antes de responder, reflita:
- Quais estratégias você conhece para resolver sistemas de equações?
- Qual delas você considera mais adequada para resolver este sistema? Por quê?
- O que você observa nas equações que pode ajudar na escolha do método?
B) Resolva o sistema, determinando os valores de x e y.
QUESTÃO 6
A biblioteca da escola recebeu um total de 250 exemplares, entre livros de ficção e livros de fábulas. Sabe-se que a quantidade de livros de ficção é quatro vezes maior do que a quantidade de livros de fábulas. Quantos livros de cada tipo foram recebidos?
| AUTORIA | CRISTIANE SOARES DE SOUZA |
| FORMAÇÃO | MATEMÁTICA – LICENCIATURA |
| COMPONENTE CURRICULAR | MATEMÁTICA |
| HABILIDADES | (EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso. |
| DESCRITOR | D34 – Identificar um sistema de equações do 1º grau que expressa um problema. |
| OBJETOS DE CONHECIMENTO | Equações de 1º grau com duas incógnitas; valor numérico de uma equação; sistema de equações de 1º grau; condição de resolução de um sistema de equações de 1º grau; métodos de resolução de um sistema de equações de 1° grau (adição, substituição e comparação). |
| REFERÊNCIAS | ROSA, Andrea Stephanie Moreira. et al. Brincando com a álgebra: o uso de jogos no ensino de sistemas de equações lineares. TANGRAN Revista de Edução Matemática. Dourados, MS, vol 3, nr 4, pp 173 – 188 (2020). Acessado na URL https://ojs.ufgd.edu.br/tangram/article/view/10968/6515 em 03/06/2025. RODRIGUES, Rodrigo Júnior. Aprendizagem significativa de sistemas de equações de 1º grau: uma sequência didática para alunos do ensino fundamental. 2021. Universidade Federal de Uberlândia. Acessado na URL https://repositorio.ufu.br/bitstream/123456789/33514/3/AprendizagemSignificativaSistemas.pdf em 03/06/2025. |

