Esta proposta de atividade de Matemática, elaborada com base no DC/GO – Ampliado, é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Triângulos semelhantes
A semelhança de triângulos é um conceito muito importante na Geometria e tem diversas aplicações práticas, como na construção civil, na navegação e até mesmo em atividades do dia a dia.

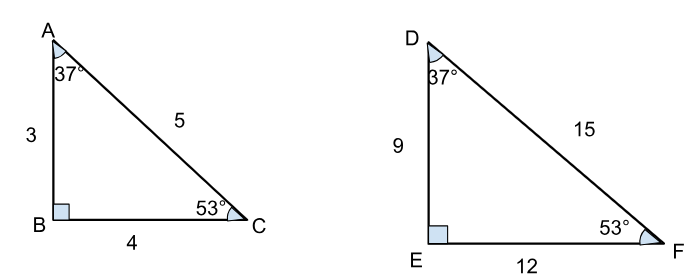
Quando dois triângulos são semelhantes, podemos comparar suas medidas usando uma razão de semelhança. Esta razão é determinada pela divisão entre as medidas de dois lados correspondentes.
Para os triângulos acima, a razão de proporção, ou razão de semelhança é
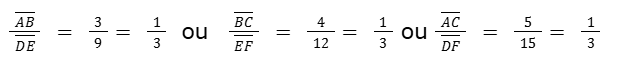
Veja que esta razão é a mesma para qualquer par de lados correspondentes dos triângulos. Por isso, os lados são proporcionais, pois seguem a mesma razão.
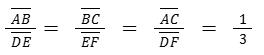
No caso acima, a razão de semelhança foi calculada do menor para o maior lado, logo é menor que 1 (13=0,333…). Trata-se portanto, de uma redução, porque as dimensões do menor triângulo equivalem a ⅓ do maior triângulo.
Se multiplicarmos as medidas de lado do maior triângulo pela razão de semelhança, vamos chegar às medidas de lado do menor triângulo. Observe:
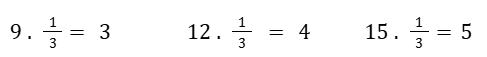
Vejamos se perímetro e área desses triângulos mantêm a mesma razão dos lados.
Perímetro:
pmenor = 3 + 4 +5 = 12 cm
pmaior= 9 + 12 + 15 = 36 cm
Razão de semelhança entre os perímetros é
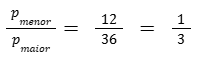
Para o perímetro, a razão de semelhança se mantém.
Área:
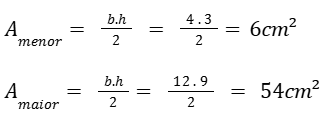
Razão de semelhança entre as áreas é
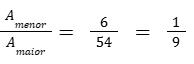
Para as áreas, a razão de semelhança é o quadrado da razão dos lados:
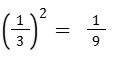
Para entender melhor como a razão de semelhança interfere no perímetro e na área, assista à videoaula “Triângulos semelhantes: o que acontece com perímetro e área?”, da professora Cristiane Souza, disponível no canal Estúdio Conexão Escola, no YouTube e veja como aplicar esses conceitos na resolução de problemas.
Agora, resolva às questão a seguir. Vale lembrar que estas atividades reforçam o descritor D5 (Reconhecer a conservação ou modificação de medidas de lado, do perímetro, da área na ampliação e/ou redução de figuras poligonais usando malhas quadriculadas) do 9º ano.
QUESTÃO 1
Dado o triângulo a seguir
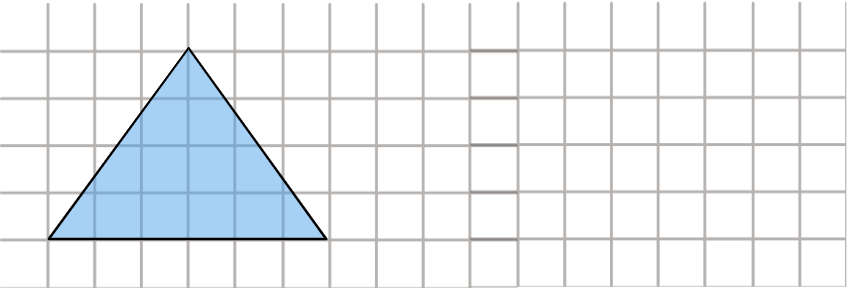
Responda:
A) Desenhe na malha o triângulo acima reduzindo seus lados à metade.
B) O perímetro do novo triângulo reduzirá na mesma proporção que os lados? Explique a sua resposta.
QUESTÃO 2
Um cliente encomendou a um marceneiro duas prateleiras em formato triangular, sendo a menor representada no desenho a seguir.
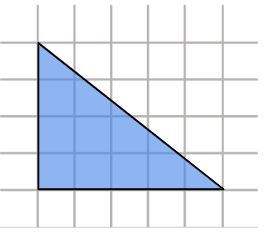
A maior prateleira foi feita com lados que medem o triplo dos lados da menor.
A) Calcule a quantidade de madeira utilizada para fabricar cada uma das prateleiras.
B) Comparando a área da menor com a da maior prateleira, o aumento foi na mesma proporção dos lados? Justifique sua resposta.
QUESTÃO 3
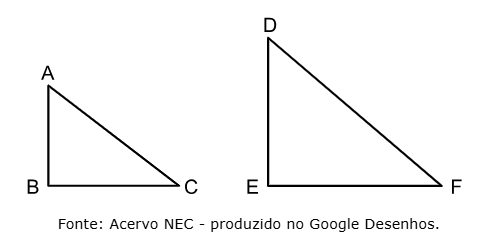
Observe os triângulos a seguir.
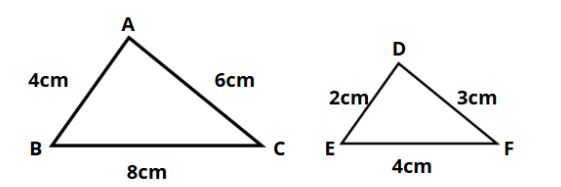
A razão de semelhança entre os triângulos ABC e DEF é igual a
(A) 1/3.
(B) 1/2.
(C) 2.
(D) 3.
QUESTÃO 4
Um canteiro tem a forma de um triângulo e está totalmente cercado por 24m de arame. O canteiro foi ampliado de modo que as medidas dos seus lados foram triplicadas. Para cercar totalmente esse novo canteiro, serão necessários
(A) 8m de arame.
(B) 48m de arame.
(C) 54m de arame.
(D) 72m de arame.
QUESTÃO 5
Os triângulos ABC e DEF são semelhantes e têm suas medidas dadas em cm.
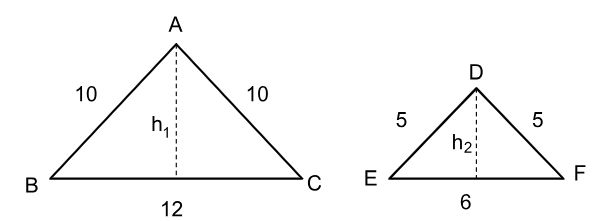
Agora responda:
A) calcule a razão entre os perímetros dos triângulos.
B) calcule a razão entre as áreas dos triângulos.
QUESTÃO 6
Os triângulos ABC e DEF são semelhantes e a razão de semelhança entre seus lados é 2:3.
Responda:
A) O perímetro do triângulo ABC é 36cm. Calcule e perímetro do triângulo DEF.
B) A área do triângulo ABC é 54cm². Calcule a área do triângulo DEF.
| Autoria: | Cristiane Soares de Souza |
| Formação: | Matemática – Licenciatura |
| Componente curricular: | Matemática |
| Habilidades: | (EF09MA12-B) Reconhecer triângulos semelhantes em situações de ampliação, congruência e redução, e as relações que existem entre seus perímetros e suas áreas. (EF06MA21) Construir figuras planas semelhantes em situações de ampliação e de redução, com o uso de malhas quadriculadas, plano cartesiano ou tecnologias digitais. |
| Descritor: | D5 – Reconhecer a conservação ou modificação de medidas de lado, do perímetro, da área na ampliação e/ou redução de figuras poligonais usando malhas quadriculadas. |
| Objetos de conhecimento: | Ampliação e redução de polígonos na malha quadriculada, conservação e modificação de medidas na ampliação e redução de polígonos (perímetro e área), semelhança de triângulos, casos de semelhanças de triângulos. |
| Referências: | SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo, Moderna, 2018. PEREIRA, Marcos Fabrício Ferreira. Uma Sequência Didática para o ensino de Semelhança de Figuras Planas. XX Ebrapen – Encontro Brasileiro de Pós-graduação em Educação Matemática, 2016. Disponível em http://www.ebrapem2016.ufpr.br/wp-content/uploads/2016/04/gd2_Marcos_Fabricio.pdf, consultado em 17/03/2025. |
