Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.

Disponível em <https://www.canva.com/design/DAF5aV7Otww/sy9UKBulgV9MF_6yWorW5g/edit?utm_content=DAF5aV7Otww&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> Último acesso em 12 de maio de 2022
Razão: Entendendo as Relações Fundamentais
A razão entre duas grandezas, como velocidade e densidade demográfica, é uma ferramenta matemática essencial para compreender e resolver problemas do mundo real. A razão é expressa como a divisão de uma quantidade pela outra, destacando a relação entre elas. Por exemplo, se um carro percorre 120 quilômetros em 2 horas, a razão entre a distância e o tempo é 120/2, resultando em uma velocidade média de 60 km/h.
Proporção: Ampliando a Perspectiva Matemática
A proporção surge quando duas razões são iguais, revelando uma equivalência entre conjuntos de grandezas. Se, no exemplo anterior, outro carro percorre 180 km em 3 horas, a razão 180/3 também é igual a 60/1, mantendo a proporção com a primeira situação. Este conceito é fundamental para explorar relações de proporcionalidade direta ou inversa entre duas ou mais grandezas.
Regras de Três Simples: Desvendando Proporções Diretas e Inversas
A regra de três simples é uma ferramenta valiosa quando lidamos com duas grandezas proporcionais. Em um contexto de proporcionalidade direta, se um aumento em uma grandeza leva a um aumento proporcional na outra, a regra de três simples se torna uma aliada na resolução de problemas. Por exemplo, se 2 metros de tecido custam R$ 10, quanto custarão 5 metros?
Para resolver esse problema utilizando a regra de três simples, podemos seguir os seguintes passos:
Passo 1: Identificar as grandezas envolvidas:
- A primeira grandeza é a quantidade de tecido, medida em metros (2 metros).
- A segunda grandeza é o custo associado a essa quantidade, em reais (R$ 10,00).
Passo 2: Estabelecer a proporção:
- Vamos criar uma proporção relacionando a quantidade de tecido ao custo:

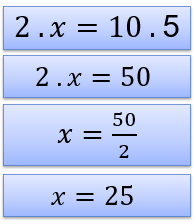
Resposta: 5 metros de tecido custarão R$ 25,00.
Dessa forma, ao utilizar a regra de três simples, conseguimos determinar que 5 metros de tecido custarão R$ 25, mantendo a proporção inicial constante. Esse método é útil para resolver problemas nos quais há uma relação proporcional entre duas grandezas.
Escalas e Divisão em Partes Proporcionais: Aplicações no Cotidiano
A compreensão de escalas é essencial em diversos contextos, desde mapas geográficos até representações gráficas. Se uma cidade possui uma densidade demográfica de 500 habitantes por km², como essa densidade seria representada em uma área de 0,5 km²? A divisão em partes proporcionais se revela como uma ferramenta valiosa nesse cenário, proporcionando uma visão clara das relações proporcionais.
Taxa de Variação: A Dinâmica do Tempo e da Mudança
A taxa de variação é uma medida crucial em problemas que envolvem mudanças ao longo do tempo. Se um tanque é preenchido a uma taxa constante, entender a relação entre a taxa de preenchimento e o tempo é vital. Por exemplo, se um tanque de 120 litros é preenchido a uma taxa de 2 litros por minuto, quanto tempo levará para encher completamente?
Contextualização Sociocultural e Ambiental: Aplicando Conceitos em Situações do Mundo Real
Ao aplicar esses conceitos em contextos socioculturais e ambientais, podemos resolver problemas do mundo real de maneira mais eficaz. Considere, por exemplo, como a densidade demográfica impacta a qualidade de vida em diferentes regiões urbanas ou como a taxa de variação em recursos naturais afeta o equilíbrio ambiental.
Conclusão: Uma Jornada Matemática na Resolução de Problemas
Resolver problemas que envolvem a razão entre grandezas distintas e aplicar regras de três simples e compostas são habilidades valiosas. Aprofundar a compreensão de conceitos como razão, proporção, escalas e taxa de variação não apenas fortalece as habilidades matemáticas, mas também oferece ferramentas essenciais para interpretar e resolver desafios complexos em diferentes áreas da vida. Ao integrar esses conhecimentos em contextos socioculturais e ambientais, ampliamos o horizonte da aplicação prática da matemática em nosso dia a dia.
Assista a videoaula da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
Ana planeja fazer uma viagem de carro e sabe que o combustível custa R$ 4 por litro. Se o veículo dela faz 12 km por litro, quanto ela gastaria para percorrer 300 km?
(A) R$ 60,00.
(B) R$ 70,00.
(C) R$ 80,00.
(D) R$ 90,00.
Questão 2
Se Carlos normalmente leva 20 minutos para percorrer 15 km até o trabalho, qual seria o tempo esperado para percorrer 30 km no mesmo percurso?
(A) 25 minutos
(B) 30 minutos
(C) 40 minutos
(D) 45 minutos
Questão 3
Renata está seguindo uma receita que pede 2 colheres de chá de sal para cada 500g de massa. Se ela está preparando 1 kg de massa, quanto sal será necessário?
Questão 4
Marcelo tem uma torneira que despeja 15 litros de água por minuto. Se ele deseja encher um balde de 30 litros, quanto tempo levará?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA07) Resolver problemas que envolvam a razão entre duas grandezas de espécies diferentes, como velocidade e densidade demográfica. (EF09MA08-A) Reconhecer o uso das regras de três simples e compostas em situações problema que envolvam relações de proporcionalidade direta ou inversa entre duas ou mais grandezas. (EF09MA08-B) Ler, interpretar, resolver e elaborar problemas que envolvam relações de proporcionalidade direta e inversa entre duas ou mais grandezas, inclusive escalas, divisão em partes proporcionais e taxa de variação, em contextos socioculturais, ambientais e de outras áreas. |

