Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Radiciação

A radiciação é usada na Matemática há algumas centenas de anos. A princípio, o cálculo da raiz quadrada de um número estava ligado à Geometria, ao determinar a medida do lado de uma área quadrada conhecida. Mais tarde, a radiciação passa a ser usada também na Álgebra, na solução de equações. Segundo a história, até então, não existia o símbolo para raiz. Este só surgiu em 1525, na Europa, com Christoff Rudolff e o utilizamos desde então.
A raiz de um número real
Chamamos de raiz de um número a qualquer, a base b que, multiplicada por ela mesma, na quantidade de vezes determinada pelo índice (n) da raiz, seja igual a a.

Os elementos de uma raiz são:

Cálculo da raiz enésima de um número real
A radiciação está ligada à potenciação. Veja!
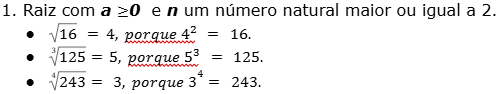
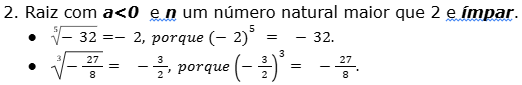
Vale lembrar que não tem solução real para as raízes de índice par de número negativo.

Propriedades da radiciação
1. Raiz do produto de dois números é igual ao produto das raízes desses mesmos números.
Genericamente:
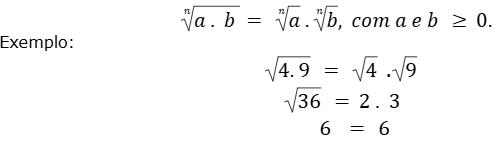
2. Raiz do quociente entre dois números é igual ao quociente das raízes desses mesmos números.
Genericamente:

3. A raiz de um número corresponde à potência de um base elevada a expoente fracionário.
Genericamente:

Operações com radicais
1. Adição e Subtração: a adição e a subtração se dá por semelhança. Por isso, somar ou subtrair números em que os radicais sejam exatamente iguais (mesmo radicando e mesmo índice de raiz).
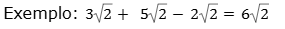
2. Multiplicação: considerando a propriedade da multiplicação, efetuar essa operação entre radicais com o mesmo índice.
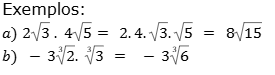
3. Divisão: a exemplo da multiplicação de radicais, efetuar a divisão entre os coeficientes das raízes e entre os radicandos das raízes, desde que tenham o mesmo índice.
Exemplo:
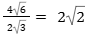
Reveja os conceitos apresentados acima, assistindo à videoaula “Cálculo da raiz de um número real”, da professora Cristiane Souza, do Canal Estúdio Conexão Escola.
Teste o seu conhecimento resolvendo a lista de atividades a seguir.
QUESTÃO 1
A raiz é uma operação matemática que corresponde a uma potência de uma base com expoente fracionário. Por exemplo
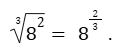
Sendo assim, a potência 27/2 corresponde à
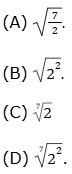
QUESTÃO 2
Resolva a expressão:
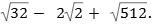
QUESTÃO 3
A simplificação de
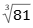
corresponde a
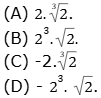
QUESTÃO 4
Um terreno tem a forma de um quadrado com área de 360m².
A) Entre quais quadrados perfeitos está 360?
B) Qual é a medida aproximada das laterais desse terreno?
C) Explique a sua estratégia para calcular a medida da lateral do terreno.
QUESTÃO 5
Considerando as propriedades dos radicais, classifique as sentenças a seguir em (V) verdadeiras ou (F) falsas.
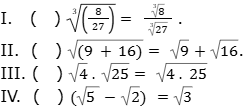
QUESTÃO 6
Um retângulo tem as dimensões apresentadas na imagem a seguir.
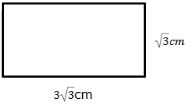
A) Qual é o perímetro deste retângulo?
B) Calcule a área do retângulo indicado.
QUESTÃO 7

| AUTORIA | CRISTIANE SOARES DE SOUZA |
| FORMAÇÃO | MATEMÁTICA – LICENCIATURA |
| COMPONENTE CURRICULAR | MATEMÁTICA |
| HABILIDADE(S): | (EF09MA03-A) Efetuar cálculos com radicais usando propriedades operatórias, inclusive racionalização de denominadores, em resolução de problemas diversos. |
| DESCRITOR(ES) | 9N1.6 Calcular o resultado de potenciação ou radiciação envolvendo números reais. 9N2.1 Resolver problemas de adição, subtração, multiplicação, divisão, potenciação ou radiciação envolvendo números reais, inclusive notação cientîfica D25 – Efetuar cálculos que envolvam operações com números racionais (adição, subtração, multiplicação, divisão, potenciação); D26 – Resolver problema com números racionais envolvendo as operações (adição, subtração, multiplicação, divisão, potenciação) |
| OBJETOS DE CONHECIMENTO | Radiciação; raiz de um número real; propriedades da radiciação; operações com raízes. |
| REFERÊNCIA | BARBOSA, Ricardo Augusto Oliveira José. Ensino de Potências e Funções Exponenciais. Universidade Federal do Mato Grosso do Sul, Programa Mestrado Profissional em Matemática em Rede Nacional. Três Lagoas/MS. 2016. Disponível na URL https://repositorio.ufms.br/bitstream/123456789/3058/1/Ensino%20de%20pot%C3%A Ancias%20e%20fun%C3%A7%C3%B5es%20exponenciais.pdf BATISTA, J. de M. .; SANTIAGO, R. V. A utilização de uma sequência didática para o ensino de Potências e Raízes . Revista de Investigação e Divulgação em Educação Matemática , [S. l.], v. 7, n. 1, 2023. DOI: 10.34019/2594-4673.2023.v7.41012. Disponível em: https://periodicos.ufjf.br/index.php/ridema/article/view/41012. Acesso em: 24 set. 2025. ARAÚJO, Weslay Vieira de. et al. Potenciação e Radiciação: as contribuições dos jogos matemáticos no processo de ensino. Revista Foco, v.17, nº 12, p.01 – 23, 2024. Disponível em https://ojs.focopublicacoes.com.br/foco/article/download/7173/5165/17330, consultado em 01/10/25. SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo. Editora Moderna, 2018. |

