Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8° Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAGEwr5Pnk0/t3To1V6yBEcnhE5ewHelxg/edit?utm_content=DAGEwr5Pnk0&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
A potenciação e a radiciação, assim como as outras operações matemáticas, são usadas na resolução de problemas de diversas áreas, desde a matemática pura até aplicações práticas em ciências, engenharia e economia. Tanto a potenciação quanto a radiciação são operações fundamentais que desempenham papéis essenciais na simplificação de expressões, na resolução de equações e na compreensão de fenômenos complexos.
A potenciação é o processo de elevar um número a uma determinada potência, representado pela notação ab, onde a é a base e b é o expoente. Essa operação nos permite calcular grandes quantidades e modelar relações exponenciais, que são comuns em situações como crescimento populacional, decaimento radioativo, juros compostos e muitas outras.
Por exemplo, ao calcular 23, estamos multiplicando o número 2 por si mesmo três vezes, resultando em 8. Essa ideia de repetição é usada em muitos contextos matemáticos e científicos, tornando a potenciação útil para modelar fenômenos naturais e artificiais.
Já a radiciação é o processo inverso da potenciação, onde encontramos a raiz de um número. Por exemplo, a raiz quadrada de 25 é 5, pois 52 = 25. A radiciação também é usada para resolver equações, simplificar expressões e calcular medidas em geometria, física e outras disciplinas.
Em certas circunstâncias, é comum encontrar expressões com radicais no denominador de frações. Para lidar com essa situação, é necessário realizar a racionalização de denominadores.
A racionalização de denominadores é uma técnica que visa simplificar expressões matemáticas, especialmente aquelas que envolvem radicais no denominador de frações. Sua função é tornar as expressões mais simples e facilitar os cálculos matemáticos.
O processo de racionalização é relativamente simples e envolve a eliminação de raízes quadradas (ou outras raízes) do denominador de uma fração. Isso é feito multiplicando tanto o numerador quanto o denominador da fração por uma expressão adequada que resulte na eliminação da raiz no denominador. Por exemplo, vamos racionalizar a fração:
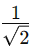
Para isso, vamos multiplicar o numerador e o denominador por:
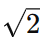
Ao fazer isso, eliminamos a raiz quadrada do denominador, obtendo uma fração simplificada e mais fácil de manipular:
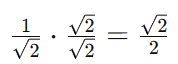
Veja que:
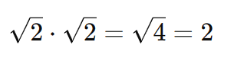
A racionalização de denominadores é utilizada em diversas áreas da matemática, incluindo equações, integração, simplificação de expressões e resolução de problemas práticos. Na simplificação de expressões algébricas que contêm radicais no denominador, a racionalização é uma etapa necessária para obter uma forma mais conveniente e manipulável da expressão. Ela é importante em problemas que envolvem cálculos com raízes, como na geometria, trigonometria e em outras áreas da matemática aplicada. Sempre que um radical estiver no denominador, devemos racionalizar.
QUESTÃO 1
Considere uma receita que pede 1/√3 xícaras de açúcar. Para preparar a quantidade correta de açúcar, você precisa de
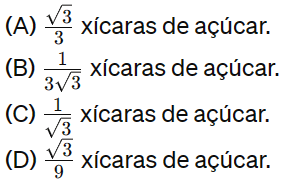
QUESTÃO 2
Ao preparar uma receita, você precisa de 1/√6 colheres de chá de tempero. A quantidade correta de tempero necessária é

QUESTÃO 3
Se o lado de um quadrado mede 1/√2 metros, qual é a área desse quadrado?
QUESTÃO 4
Se um terreno retangular tem um comprimento de 1/√5 metros e uma largura de 1/√2 metros, qual é a área total do terreno?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF08MA02-A) Reconhecer a importância da potenciação e da radiciação na resolução de problemas, fazendo uso de suas propriedades operatórias, incluindo a racionalização de denominadores, além de compreendê-las como operações inversas. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |

