Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9° Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAF_gnPjsYY/vTem8qEIWZw5uo9oeuW4CA/edit?utm_content=DAF_gnPjsYY&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 20 de março de 2024.
A racionalização de denominadores envolve a modificação de uma expressão algébrica para que o denominador se torne um valor racional, ou seja, livre de raízes ou expressões irracionais. Este processo é necessário na simplificação de frações algébricas para torná-las mais adequadas para análise e interpretação. Isso é especialmente útil ao resolver equações e inequações algébricas que envolvem raízes ou outras expressões irracionais.
A ideia principal por trás da racionalização de denominadores é eliminar as raízes quadradas ou outras expressões irracionais presentes no denominador, tornando a expressão mais fácil de manipular e entender. Isso é feito multiplicando o numerador e o denominador por uma expressão conveniente que elimine as raízes no denominador. Veja um exemplo onde o número raiz quadrada de 2 está no denominador de uma fração, Para racionalizar o denominador, multiplicamos o numerador e o denominador por raiz quadrada de 2:
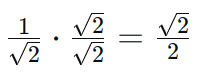
Lembre-se que:
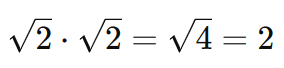
Veja outro exemplo:
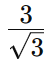
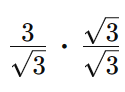
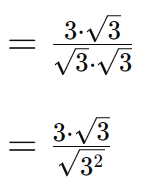
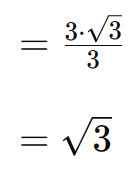
Podemos então concluir que para racionalizar um denominador com uma raiz quadrada, como raiz quadrada de 2 ou de 3, multiplicamos o numerador e o denominador pela raiz correspondente. Essa raiz escolhida para multiplicação é chamada de conjugado da raiz presente no denominador.
Por exemplo, se o denominador for raiz quadrada de 2, multiplicamos tanto o numerador quanto o denominador por raiz quadrada de 2. Isso elimina a raiz quadrada do denominador e nos permite obter um denominador racional.
Que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
A professora de Ana escreveu uma fração no quadro para ser racionalizada. Podemos concluir que o resultado obtido ao resolver corretamente foi

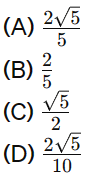
QUESTÃO 2
Após calcular a hipotenusa de um triângulo retângulo, Pedro chegou ao resultado indicado na figura. Podemos afirmar que esse valor corresponde a
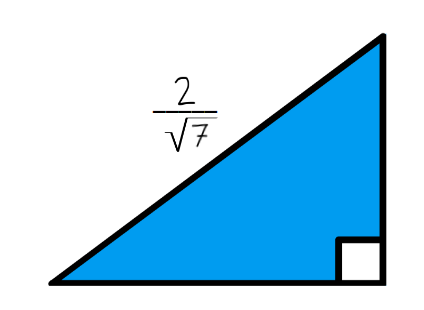
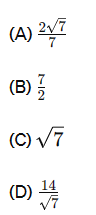
QUESTÃO 3
Explique o processo de racionalização de denominadores e por que é importante na simplificação de expressões irracionais.
QUESTÃO 4
Explique por que a racionalização de denominadores é necessária ao resolver problemas envolvendo triângulos retângulos e a hipotenusa.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA03-A) Efetuar cálculos com radicais usando propriedades operatórias, inclusive racionalização de denominadores, em resolução de problemas diversos. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |

