Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8° Ano do Ensino Fundamental – Anos Finais.
Disponível em: <https://www.canva.com/design/DAF1eBU1guk/ULyxCB_asPREtrYDOAqs8w/edit?utm_content=DAF1eBU1guk&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 28 de novembro de 2023.
Os produtos notáveis desempenham um papel crucial no estudo da álgebra, pois são usados para simplificar expressões e revelar padrões. Três deles merecem atenção especial: o quadrado da soma de dois termos, o quadrado da diferença de dois termos e o produto da soma pela diferença de dois termos.
Quadrado da Soma de Dois Termos: (a + b)²
Sabemos que o quadrado de um número é o mesmo que multiplicar esse número por ele mesmo, então: (a + b)² = (a + b) . (a + b)
Vamos fazer essa multiplicação usando a propriedade distributiva:
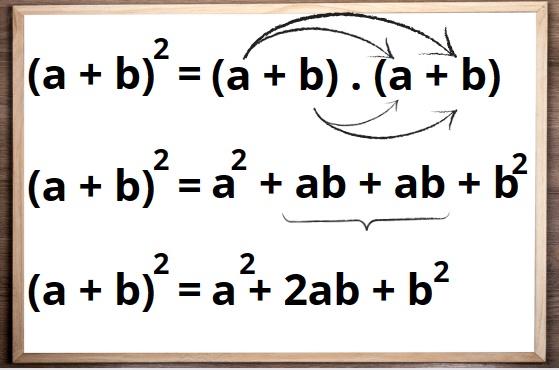
Então, a soma de dois termos elevada ao quadrado é igual ao quadrado do primeiro termo mais o dobro do produto dos dois termos mais o quadrado do segundo termo.
(a + b)² = a² + 2ab + b²
Quadrado da Diferença de Dois Termos: (a – b)²
Podemos notar uma similaridade com o quadrado da soma, mas com sinal distinto. Então, também vamos resolver usando a propriedade distributiva. Veja:
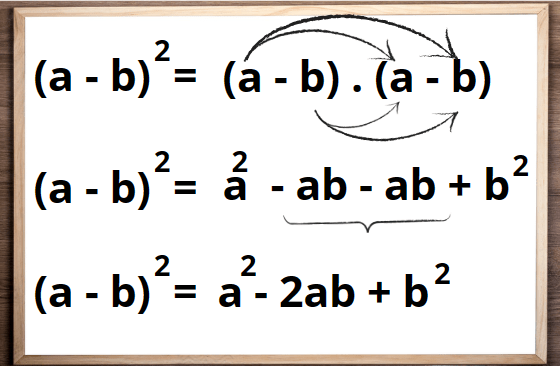
Concluímos então que, a diferença de dois termos elevada ao quadrado é igual ao quadrado do primeiro termo menos o dobro do produto dos dois termos mais o quadrado do segundo termo.
(a – b)² = a² – 2ab + b²
Produto da Soma pela Diferença: (a + b)(a – b)
O terceiro destaque nos produtos notáveis é o produto da soma pela diferença de dois termos, representado por (a + b)(a – b). Ao multiplicar esses dois binômios, a expressão resultante é a diferença dos quadrados dos termos individuais: a² – b². Podemos chegar a esse resultado, assim como nos outros casos, usando a propriedade distributiva:
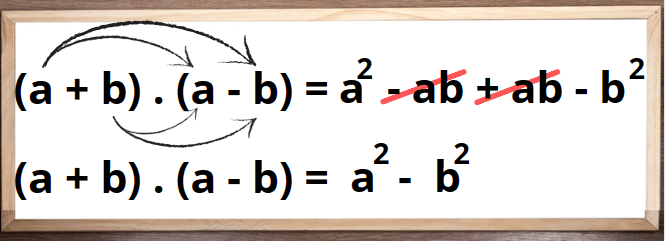
Em resumo, os produtos notáveis oferecem um conjunto de ferramentas poderosas para simplificar e desvendar padrões em expressões algébricas. O quadrado da soma, o quadrado da diferença e o produto da soma pela diferença de dois termos são pilares fundamentais na caixa de ferramentas matemáticas, proporcionando clareza e eficiência em uma variedade de contextos.
Agora que você , que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Ana está reformando seu quarto e planeja instalar azulejos em forma de quadrados. Se a largura da parede é representada por x + y e o comprimento por x – y, como Ana expressaria a área total, considerando que ela quer cobrir toda a parede?
(A) x² – 2xy + y²
(B) x² + 2xy + y²
(C) x² – 2xy – y²
(D) x² – y²
QUESTÃO 2
João está cultivando plantas em seu jardim. Ele está usando uma parte quadrada do seu jardim onde os lados medem y + 3. Que expressão algébrica representa a área do terreno de cultivo?
(A) y² – 6y + 9
(B) y² – 6y – 9
(C) y² + 6y + 9
(D) y² + 6y + 6
QUESTÃO 3
A professora de Aline deixou no quadro o seguinte desafio:
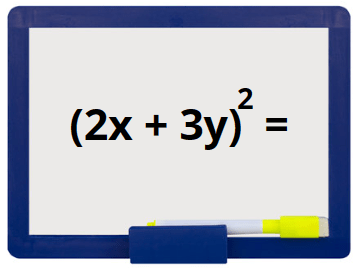
Qual é a solução correta desse desafio?
QUESTÃO 4
Ao desenvolver um dos produtos notáveis, o resultado obtido foi r² + 18r + 81. Quais eram o primeiro e o segundo termo para que a solução fosse essa?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF08MA06-C) Reconhecer e aplicar os produtos e quocientes notáveis para desenvolver as operações envolvendo monômios e polinômios, como adição, subtração, multiplicação e divisão exata entre monômios e polinômios. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |
