Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8º Ano do Ensino Fundamental – Anos Finais.
PRINCÍPIO MULTIPLICATIVO DA CONTAGEM
A ação de contar faz parte do nosso cotidiano. Contar os elementos, objetos de forma individualizada, um a um. Mas existem situações em que precisamos contar possibilidades de combinações em eventos que acontecem em sequência.
Veja este exemplo clássico: quantos looks (combinações de roupa) podem ser montados 3 camisetas e 2 calças diferentes?
Fonte: Possibilidades de combinações – Acervo NEC – produzido no canva.com
Observe que, combinando cada camiseta com cada calça, teremos 6 combinações diferentes de se vestir.
Veja esta outra situação. Em uma lanchonete, o cliente pode montar seu sanduíche escolhendo um tipo de pão, um tipo de molho e um tipo de recheio. As opções são
- 2 tipos de pães: baguete e integral;
- 2 tipos de molhos: maionese e mostarda;
- 2 tipos de recheios: presunto com queijo e vegetariano.
Quantas combinações de sanduíches diferentes podem ser montadas?
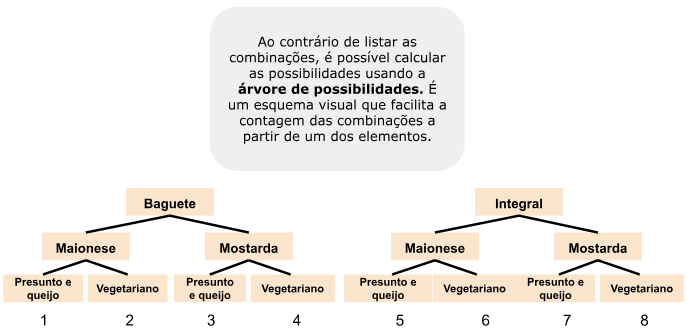
É possível montar 8 sanduíches diferentes. Observe que o resultado é o igual ao produto entre as quantidades de pães, molhos e recheios disponíveis na lanchonete.
2 x 2 x 2 = 8
Pelo princípio fundamental da contagem ou princípio multiplicativo, quando temos diferentes etapas de escolha e cada etapa apresenta múltiplas opções, o número total de combinações possíveis é obtido multiplicando a quantidade de escolhas em cada etapa.
Essas estratégias tornam a contagem mais eficiente e organizada e podem ser aplicadas em outras situações como como criar senhas, planejar rotas ou trajetos, organizar tabelas de campeonatos.
Para reforçar os conceitos apresentados acima, assista ao vídeo “Princípio da contagem”, da professora Cristiane, disponível no canal Estúdio Conexão Escola, no YouTube.
Hora da prática! Resolva as questões abaixo.
QUESTÃO 1
Suponha que, para viajar de Goiânia a Pirenópolis de ônibus, você possa escolher entre 2 companhias, cada uma com 4 horários de saída. Quantas opções diferentes de viagem são possíveis?
(A) 2
(B) 4
(C) 6
(D) 8
QUESTÃO 2
Para aumentar a segurança, os fabricantes de malas adotaram um tipo de cadeado com segredo de 3 números, de 0 a 9. Esses números são escolhidos pelo próprio cliente, podendo repetir, como mostra a figura.
Fonte: Mala com segredo – canva.com.
Considerando essas condições, quantas senhas diferentes podem ser criadas?
QUESTÃO 3
Em um jogo, cada jogador lança um par de dados para o alto e a soma dos números que aparecem voltados para cima determina a quantidade de pontos do jogador naquela rodada. Cada dado possui seis faces numeradas de 1 a 6.
O total de combinações diferentes de resultados que podem ocorrer ao lançar dois dados é igual a
(A) 7.
(B) 15.
(C) 36.
(D) 49.
QUESTÃO 4
Para ir de casa para escola, Jeane percorre um trecho de ônibus e o trecho restante, caminhando até a escola. As opções de trajetos para Jeane estão ilustradas na figura a seguir.
Fonte: Trajeto casa para escola – Acervo NEC – produzido no canva.com
Analisando a imagem, responda:
A) Quantas opções de ônibus Jeane tem para ir à escola?
B) O percurso final Jeane faz caminhando. Quantas opções de caminhos Jeane tem para chegar até a escola depois do ônibus?
C) Quantas opções Jeane tem para ir de casa até a escola?
| Autoria: | Cristiane Soares de Souza |
| Formação: | Matemática – Licenciatura |
| Componente curricular: | Matemática |
| Habilidade(s): | (EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1. |
| Objeto(s) de conhecimento: | Princípio multiplicativo ou princípio fundamental da contagem; Árvore de possibilidades. |
| Referência(s): | Araribá mais: Matemática: organizadora Editora Moderna, obra coletiva concebida, desenvolvida e produzida pela Editora Moderna. Editores responsáveis: Mara Regina Garcia Gay, Willian Raphael Silva. 1ª Edição, São Paulo, 2018. EUGÊNIO, Robson da Silva. Letramento probabilístico nos anos finais do ensino fundamental: um processo de formação dialógica com professores de matemática. / Eugênio Robson da Silva. – Recife, 2019. Disponível em URL https://repositorio.ufpe.br/handle/123456789/38245, consultado em 10/03/2025. |

