MATEMÁTICA – POTÊNCIAS COM NÚMEROS REAIS

Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.

Potências

O uso da potência é muito comum na Matemática. E não é um conceito novo. Como muitos outros conceitos da Matemática, as potências surgiram há alguns milhares de anos e como uma necessidade: representar números muito grandes. 

A potência está associada à multiplicação de um mesmo número (chamado de base) por ele mesmo, tantas vezes quanto indica o expoente. 

Por exemplo, ao contrário de escrever 4 x 4 x 4, podemos usar a notação de potência, 4³. 

De modo geral, a potência é 

a^b = a x a x a x a… x a, 

com a número real diferente de zero. 

A princípio, o cálculo de potências considerava apenas expoentes naturais, como 1, 2, 3, etc. Com os avanços da Matemática, passou-se a considerar expoentes negativos, zero, fracionários ou decimais, ou seja, números reais. 

Vejamos algumas potências características

A) 2⁰ = 1, todo número elevado a expoente zero, é igual a 1. 

B) 3¹ = 3, todo número elevado a expoente um, é igual a ele mesmo. 

C) 1¹⁰ = 1, o número 1 elevado a qualquer expoente é igual a ele mesmo. 

D) Base, elevada a expoente negativo, inverte-se a base e troca o sinal do expoente:

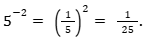
E) Base, elevada a expoente fracionário, é equivalente a uma raiz com

• radicando da raiz é a base;
• índice da raiz corresponde ao denominador da fração;
• expoente da base corresponde ao numerador da fração.

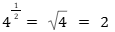
Genericamente

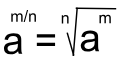
Propriedades das potências:

A) Multiplicação de potências de bases iguais: conservar a base e somar os expoentes. 

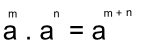
B) Divisão de potências de bases iguais: conservar a base e diminuir os expoentes.

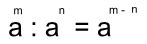
C) Potência de potência: conserva a base e multiplica os expoentes.

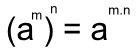
D) Potência de produto: o expoente se distribui em relação à multiplicação.

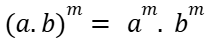
E) Potência de quociente: o expoente se distribui em relação ao quociente.

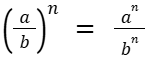
As potências em contextos reais:

As potências podem ser usadas 

• para representar o crescimento populacional de uma colônia de bactérias;
  
• no cálculo de juros compostos, em que o valor de uma dívida ou investimento aumenta de forma exponencial;
  
• na informática, para representar unidades  de medida como kilobyte, megabyte, gigabyte, terabyte.
• no uso de notação científica para escrever números muito grandes (como a distância da Terra ao Sol) ou muito pequenos (como o tamanho de uma célula).

Reveja os conceitos apresentados acima, assistindo à videoaula “Potência: conceito e propriedades”, da professora Cristiane Souza, do Canal Estúdio Conexão Escola.

Teste o seu conhecimento resolvendo a lista de atividades a seguir.

QUESTÃO 1

Em um estudo científico, os pesquisadores observaram que uma colônia de bactérias crescia de forma constante: a cada hora, o número de bactérias dobrava.

Se, no início do estudo, a colônia tinha 200 bactérias, com 2 horas de observação, o número de bactérias era igual a 

(A) 200.             

(B) 400.                   

(C) 600.               

(D) 800.

QUESTÃO 2

Para medir a capacidade de armazenamento dos computadores, a unidade básica é o byte. Nesse sistema, existem unidades maiores, como o kilobyte (KB) e o megabyte (MB).

Cada unidade é 1024 vezes maior que a anterior, e sabemos que 1024 = 2¹⁰. Assim,

• 1KB (kilobyte) = 2¹⁰ bytes e 
• 1MB (Megabyte) = 2¹⁰ KB. 

Dessa forma, 1 MB corresponde a: 

(A) 2²⁰ bytes.

(B) 2³⁰ bytes. 

(C) 2⁴⁰ bytes.

(D) 2⁵⁰ bytes. 

QUESTÃO 3

Leia com atenção as sentenças a seguir e classifique-as em (V) verdadeira ou (F) falsa. 

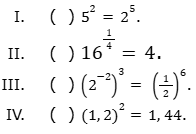
QUESTÃO 4

Usando as propriedades da potenciação, escreva os resultados na forma de uma única potência:

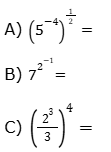
QUESTÃO 5

Resolva a expressão

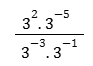
QUESTÃO 6

Uma atividade sobre potência propunha a resolução de (2²x 3)².

Jean apresentou a seguinte solução:

(2²x 3)² = (2²)² x 3² = 2⁴ x 3² =16 x 9 = 144

Você concorda com a solução apresentada por Jean? Use as propriedades de potência para justificar a sua resposta. 

AUTORIA	CRISTIANE SOARES DE SOUZA
FORMAÇÃO	MATEMÁTICA – LICENCIATURA
COMPONENTE CURRICULAR	MATEMÁTICA
HABILIDADE(S)	(EF09MA03-C) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários, em situações diversas.
DESCRITOR(ES)	9N1.6 Calcular o resultado de potenciação ou radiciação envolvendo números reais. 9N2.1 Resolver problemas de adição, subtração, multiplicação, divisão, potenciação ou radiciação envolvendo números reais, inclusive notação cientîfica D25 – Efetuar cálculos que envolvam operações com números racionais (adição, subtração, multiplicação, divisão, potenciação); D26 – Resolver problema com números racionais envolvendo as operações (adição, subtração, multiplicação, divisão, potenciação)
OBJETOS DE CONHECIMENTO	Potenciação; propriedades das potências; potência com exponente negativo e fracionário; operações com potências.
REFERÊNCIA	BARBOSA, Ricardo Augusto Oliveira José. Ensino de Potências e Funções Exponenciais. Universidade Federal do Mato Grosso do Sul, Programa Mestrado Profissional em Matemática em Rede Nacional. Três Lagoas/MS. 2016. Disponível na URL https://repositorio.ufms.br/bitstream/123456789/3058/1/Ensino%20de%20pot%C3%A Ancias%20e%20fun%C3%A7%C3%B5es%20exponenciais.pdf  BATISTA, J. de M. .; SANTIAGO, R. V. A utilização de uma sequência didática para o ensino de Potências e Raízes . Revista de Investigação e Divulgação em Educação Matemática , [S. l.], v. 7, n. 1, 2023. DOI: 10.34019/2594-4673.2023.v7.41012. Disponível em: https://periodicos.ufjf.br/index.php/ridema/article/view/41012. Acesso em: 24 set. 2025. ARAÚJO, Weslay Vieira de. et al. Potenciação e Radiciação: as contribuições dos jogos matemáticos no processo de ensino. Revista Foco, v.17, nº 12, p.01 – 23, 2024. Disponível em https://ojs.focopublicacoes.com.br/foco/article/download/7173/5165/17330, consultado em 01/10/25.  SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo. Editora Moderna, 2018.