Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 5º Ano do Ensino Fundamental – Anos Iniciais.
Porcentagem
A porcentagem está presente em várias situações do cotidiano:
- no comércio indicando aumentos ou descontos sobre um valor;
- em dados indicando parte de uma quantidade;
- para indicar carga de bateria, entre outras coisas.
A porcentagem surgiu porque as pessoas precisavam calcular partes de um valor, como dinheiro, alimentos e impostos.
Há muitos séculos atrás, os romanos cobravam impostos calculando a centésima parte da mercadoria comercializada. Usavam a divisão por 100 porque era um número fácil de dividir. O símbolo de % só foi usado muitos anos depois.
O que é porcentagem?
A porcentagem ou por cento indica quantas partes de 100 vamos utilizar. Ou seja, algo foi dividido em 100 partes iguais e vamos contar apenas algumas dessas partes.
Exemplo: 10%, significa que vamos contar 10 a cada 100.
Representações de porcentagem
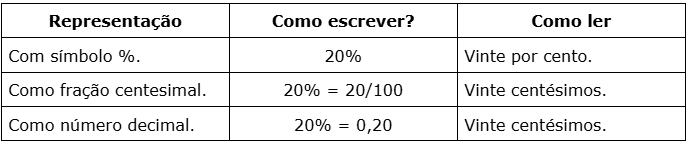
Uma porcentagem pode ser representada por valor na forma de
- Com símbolo %:
O número seguido do símbolo %. Por exemplo: 20% que significa: a cada 100 vamos contar 20.
- Na forma de fração centesimal ou com denominador 100.
Exemplo: 20% = 20/100.
- Na forma de número decimal por se tratar de uma divisão por 100.;
Exemplo: 20% = 20/100 ou 0,2.
Cálculo de porcentagem
Para resolver um problema com porcentagem, podemos usar qualquer uma de suas representações. Vejamos alguns exemplos.
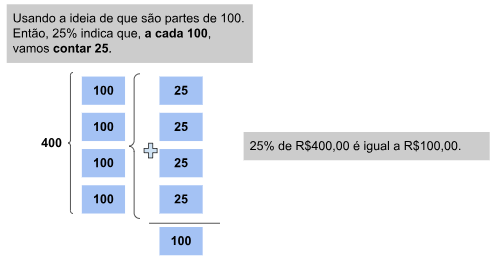
1. Eu gastei 25% de R$400,00 com a compra de uma roupa. Qual foi o valor desta roupa?
2. Uma mochila custa R$80,00. Se for paga em dinheiro, tem 20% de desconto. Qual é o valor do desconto?
Vamos calcular 20% de 80 reais usando as frações equivalentes.
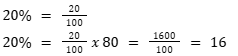
O valor do desconto será de R$16,00.
3. Dos 95 estudantes de uma escola, 60% gosta de praticar esportes. Qual é o número de estudantes que gostam de praticar esportes?
Vamos calcular usando a forma decimal.
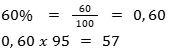
57 estudantes gostam de praticar esportes.
A porcentagem é utilizada em muitas situações do cotidiano. Por isso é importante compreender seu conceito e sua aplicação. E para entender melhor a relação de equivalência entre porcentagem, fração e número decimal, assista à videoaula “Porcentagem, fração e decimal: uma relação de equivalência”, da professora Cristiane Souza, do Canal Estúdio Conexão Escola. Clique aqui!
Agora é só praticar o que aprendeu.
Bom trabalho!
QUESTÃO 1
Na calculadora, Mariana apertou a seguinte sequência de teclas:

O valor que apareceu na tela da calculadora foi
(A) 320,0.
(B) 32.
(C) 3,2.
(D) 0,32.
QUESTÃO 2
Na entrada de uma loja foi colocada esta faixa:

Lendo essa faixa, podemos afirmar que qualquer produto na loja será vendido
(A) pelo dobro do preço.
(B) pelo triplo do preço.
(C) pela metade do preço.
(D) pela terça parte do preço.
QUESTÃO 3
Um valor em porcentagem pode ser escrito na forma de fração com denominador 100, ou fração centesimal, como no exemplo:
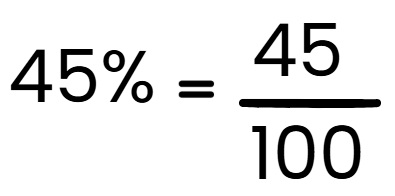
Agora, complete as igualdades abaixo:
A) 7% =_______
B) ______= 34/100
C) ______ = 56/100
D) 12% = ______
QUESTÃO 4
Paulo e Luiz estão jogando videogame.

Agora responda:
A) Se Paulo pegar o bônus, com quantos por cento de energia ficará?
B) Paulo tinha 500 pontos e, ao pegar o bônus, sua pontuação aumentou em 30%. Quantos pontos Paulo ganhou com o bônus?
QUESTÃO 5
Jean investiu R$2.500,00 em um banco. Em um ano, o banco vai pagar 20% desse valor como rendimento. Quanto este valor renderá em um ano?
| AUTORIA: | Cristiane Soares de Souza |
| FORMAÇÃO: | Matemática – Licenciatura |
| COMPONENTE CURRICULAR: | Matemática. |
| OBJETOS DE CONHECIMENTO / CONTEÚDOS: | Noção de porcentagem; fração centesimal; forma decimal; cálculo da porcentagem de um valor; idéia de acréscimo e desconto. |
| HABILIDADES: | (EF05MA06-B) Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, à décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros. (EF05MA06 – C) Solucionar problemas envolvendo cálculo de 10%, 25%, 50%, 75% e 100%, utilizando diferentes estratégias de resolução, enfatizando o cálculo mental. |
| DESCRITOR(ES): | 5N2.7 – Resolver problemas que envolvam 10%, 25%, 50%, 75% e 100%, associando essas representações, respectivamente, à décima parte, quarta parte, metade, três quartos e um inteiro. D26 – Resolver problemas envolvendo noções de porcentagem (25%, 50%, 100%) |
| REFERÊNCIA: | MELO, Pablo Henrique do Nascimento. et al. A construção do conceito de porcentagem nos anos iniciais. CONEDU – Congresso Nacional de Educação. Disponível em https://www.editorarealize.com.br/editora/anais/conedu/2024/TRABALHO_COMPLETO_ EV200_MD1_ID12366_TB4733_23102024224920.pdf, acessado em 05/11/25. SILVA, Zeneide. PASSOS, Célia. Eu gosto m@is: Matemática. 5º ano. 5ª edição. São Paulo / IBEP. |

