Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAGImj_Qtzw/H6hBs4-rbSNA78U9wyfVbg/edit?utm_content=DAGImj_Qtzw&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
Monômios e polinômios são usados na álgebra e em diversas aplicações matemáticas, como na física, engenharia, economia e outras áreas. Os monômios e polinômios são a base da álgebra e aparecem em inúmeras fórmulas e funções matemáticas. Eles são usados para modelar fenômenos no mundo real, desde trajetórias de objetos em movimento até cálculos financeiros. Vamos relembrar o que são monômios:
Monômios
Um monômio é uma expressão algébrica que consiste em um único termo. Ele é formado por um coeficiente (um número) e uma parte literal (uma ou mais variáveis elevadas a expoentes inteiros não negativos).
Exemplos de Monômios:
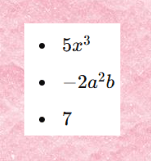
Componentes de um Monômio:
Coeficiente: O número que multiplica a parte literal.
Parte Literal: As variáveis com seus respectivos expoentes.
Grau: A soma dos expoentes das variáveis.
Exemplo:

Polinômios
Um polinômio é uma expressão algébrica que consiste em uma soma de monômios. Os polinômios podem ser classificados pelo número de termos que possuem:
Binômio: Polinômio com dois termos.
Trinômio: Polinômio com três termos.
Polinômio Geral: Polinômio com mais de três termos.
Exemplo de Polinômios:

Grau do Polinômio: O maior grau entre todos os monômios que compõem o polinômio.
Exemplo:

Exemplos Resolvidos
Exemplo 1: Identificar componentes de um monômio

Exemplo 2: Identificar componentes de um polinômio

Exemplo 3: Classificar polinômios pelo número de termos

Exemplo 4: Grau de um polinômio

Agora que você , que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
A depreciação de um equipamento pode ser modelada pelo polinômio 4a2 − 6a + 2, onde a é o número de anos. Quantos termos possuem esse polinômio?
(A) 1
(B) 2
(C) 3
(D) 4
QUESTÃO 2
A produção de uma fábrica é representada pela expressão 10y + 15, onde y é o número de dias. Qual é o grau desse polinômio?
(A) 0
(B) 1
(C) 2
(D) 3
QUESTÃO 3
Uma empresa de tecnologia modela seu lucro trimestral com a expressão x2 − 2x + 1 , onde x é o número de trimestres. Qual é a parte literal do termo de maior grau?
QUESTÃO 4
A área de um terreno retangular é representada pelo produto de suas dimensões, dado por 2x ⋅(3x+5). Qual é o coeficiente, a parte literal e o grau do resultado dessa expressão?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF08MA06-B) Identificar monômios e polinômios (binômio, trinômio, entre outros) com os seus respectivos graus, coeficientes e partes literais. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |
