Esta proposta de atividade de Matemática, elaborada com base no DC/GO – Ampliado, é destinada aos estudantes do 5º Ano do Ensino Fundamental – Anos Iniciais.
Plano Cartesiano: localização
Localização
Quando queremos explicar onde alguma coisa está ou como chegar a um lugar, usamos a ideia de localização.
Localizar significa dizer a posição de algo ou alguém em um determinado espaço.
“A escola está à esquerda da padaria.”
O ponto de referência ajuda a entender onde algo está comparando com outro lugar conhecido.
O que é plano cartesiano?
Na Matemática, uma forma mais precisa de localização é o plano cartesiano.
O plano cartesiano é um sistema de coordenadas formado por dois eixos principais que são numerados:
- um horizontal (eixo x): mostra os movimentos para a direita ou para a esquerda;
- outro vertical (eixo y): mostra os movimentos para cima ou para baixo.
O ponto onde esses dois eixos se cruzam é chamado de origem, e tem as coordenadas (0, 0).
Outras linhas imaginárias horizontais e verticais dividem o plano cartesiano como uma malha quadriculada. A posição do ponto é o encontro da linha horizontal com a linha vertical.
Como indicar a posição de um ponto no plano cartesiano?
Para indicar a posição, usamos um par de números chamado de par ordenado (x, y), sempre nesta ordem. Esse par ordenado mostra quanto o ponto se moveu na horizontal e vertical em relação à origem.
- O primeiro número (x) mostra o movimento horizontal, quantas unidades o ponto moveu para o lado (direita ou esquerda).
- O segundo número (y) mostra o movimento vertical, quantas unidades o ponto subiu ou desceu.
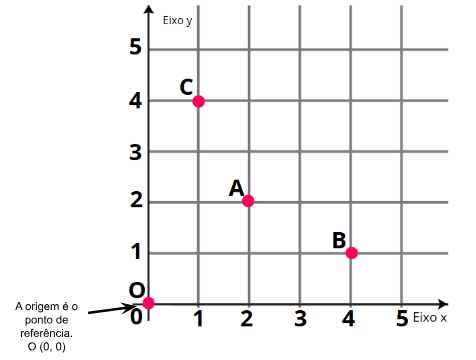
Por exemplo:
- A (2, 2);
- B (4, 1);
- C (1, 4).
Deslocamento no plano:
O ponto pode se mover no plano cartesiano tanto na horizontal (esquerda ou direita) quanto na vertical (subir ou descer). Quando o ponto se move, sua posição muda, e os números que indicam onde ele está (as coordenadas) também mudam.
Por exemplo:
O ponto B na imagem acima está em (4, 1).
Se ele andar 2 unidades para esquerda (horizontal) e 2 para cima (vertical), sua nova posição será (2, 3).
Sua nova posição será (2, 3).
Agora, resolva os exercícios a seguir.
QUESTÃO 1
Observe a imagem do quarto de Beto.
Use o banco de palavras para completar as frases e assim localizar alguns objetos no quarto de Beto, de acordo com o ponto de referência em destaque.
A) O violão está __________ do gaveteiro.
B) O skate está __________ da cama.
C) O gato está ___________ da bola.
D) A mochila está ___________ da mesa.
QUESTÃO 2
Na imagem a seguir foi colocado um sistema de coordenadas. As colunas estão identificadas por letras e as linhas por números.
Agora, use esse sistema de coordenadas para localizar na imagem, os elementos citados abaixo. Escreva a posição deles usando um par ordenado formado por (letra, número).
A) Onde está o sol?
B) Qual é a posição da bola de basquete?
C) E a corda, onde está?
D) Qual é a localização da cesta de basquete?
E) Qual é a localização da criança que está no colchonete?
QUESTÃO 3
A professora está organizando o mapa da sala de aula em uma planilha no computador. Ela observa onde cada aluno costuma sentar e escreve os nomes nas células da planilha.
A planilha é como uma tabela.
- As colunas são marcadas com letras (A, B, C…).
- As linhas são marcadas com números (1, 2, 3…).
A posição do aluno corresponde ao endereço da célula (letra da coluna e o número da linha) onde seu nome será escrito. Por exemplo:
- A1 = Caio
- B3 = Carlos
Então, na célula C2 estará o nome de
(A) Léo.
(B) Júlia.
(C) Felipe.
(D) Ana.
QUESTÃO 4
Andreia desenhou um plano cartesiano em uma malha quadriculada e marcou alguns pontos. Cada ponto tem um par de números, chamado de par ordenado (x, y).
- O x mostra a posição do ponto na horizontal.
- O y mostra a posição do ponto na vertical.
Agora responda:
A) usando par ordenado (x, y), qual é a posição do ponto A?
B) qual ponto ocupa a posição (1, 4)?
C) movendo o ponto B, 1 unidade para direita e 2 unidades para cima, qual é a sua nova posição?
D) qual ponto ocupa a posição (5,5)?
QUESTÃO 5
As afirmações abaixo se referem ao plano cartesiano. Leia cada uma delas com atenção e, depois, classifique-as em (V) verdadeira ou (F) falsa.
A) ( ) O ponto (0,0) é chamado de origem.
B) ( ) O eixo y é o eixo horizontal.
C) ( ) No plano cartesiano, usamos sempre a ordem (x, y).
D) ( ) No par ordenado (3,4), x = 3 e y = 4.
QUESTÃO 6
Em um plano cartesiano está marcado o ponto A de coordenadas (4,2). Este ponto foi movido 2 unidades para a esquerda e 1 unidade para cima. As novas coordenadas do ponto A são
(A) (2, 4).
(B) (2, 3).
(C) (5, 2).
(D) (5, 4).
| Autoria: | Cristiane Soares de Souza |
| Formação: | Matemática, licenciatura. |
| Componente Curricular: | Matemática |
| Objetos de conhecimento: | Noção de plano cartesiano com a malha quadriculada; localização de elementos no plano cartesiano; ideia de par ordenado; representação de ponto no plano cartesiano e deslocamentos no plano cartesiano. |
| Habilidade: | (EF05MA14-B) Utilizar diferentes representações para a localização de objetos no plano, como mapas, células em planilhas eletrônicas e coordenadas geográficas, a fim de desenvolver as primeiras noções de coordenadas cartesianas. |
| Descritor: | D1 – Identificar a localização / movimentação de objeto em mapas, croquis e outras representações gráficas. |
| Referências: | SOUZA, Joamir Roberto de. SOUZA, Maria Angélica Reghin de. Entrelaços: Matemática, 5º ano, ensino fundamental, anos iniciais. 1ª edição / São Paulo. FTD 2021. SILVA, Zeneide. PASSOS, Célia. Eu gosto m@is: Matemática. 5º ano. 5ª edição. São Paulo / IBEP. ARQUIERES, Darling Domingos. et al. Proposta de uma sequência didática com uso do “plano cartesiano manipulável”. Disponível na URL https://revistavalore.emnuvens.com.br/valore/article/download/1056/831, acessado em 10/04/25. |