Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento F (6º ano) do Ciclo da adolescência foi veiculada na TV no dia 26/04/2021 (Segunda-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.

Nesta atividade, você estudante do 6º ano, vai reconhecer as operações matemáticas básicas de: adição, subtração, multiplicação, divisão, a fim de estabelecer relações entre os múltiplos de um número natural e os divisores de um número natural.
Assista a videoaula a seguir com a temática: Números e operações
Olá estudante do sexto ano, nesta atividade você vai aprender sobre:
- Operações de: adição, subtração, multiplicação, divisão, potenciação e radiciação de números naturais;
- Os divisores de um número natural;
- Os múltiplos de um número natural;
- Estratégias para determinar o maior divisor comum de dois ou mais números e o menor múltiplo comum de dois ou mais números naturais.
Para iniciar os estudos, vamos definir juntos algumas estratégias para resolver problemas que envolvam as operações matemáticas:
Exemplo 1. Adição – A quantidade de meninos de uma turma de sexto ano é 13 e a quantidade de meninas é 12. Qual é a soma total de alunos dessa turma de sexto ano?
Para resolver o problema basta fazer o algoritmo da adição:

Logo, a quantidade de estudantes nesta turma de 6º ano será 25.
Os problemas de adição geralmente possuem comandos como: juntar, acrescentar, agrupar e somar.
Exemplo 2. Subtração – Pedro tinha 35 bolinhas de gude e durante uma partida, perdeu para o seu amigo João 12 de suas bolinhas. Com quantas bolinhas de gude Pedro ficou, após a perda?
Para resolver o problema, utiliza-se o algoritmo da subtração:

Logo, a quantidade de bolinhas de gude que restou a Pedro foi 23.
Os problemas relacionados à subtração possuem comandos como: subtrair, retirar, perder, completar quantidades, comparar, diferença entre outros.
Exemplo 3. Multiplicação – Tiago foi ao supermercado e comprou 5 pacotes de bolacha, cada uma custando R$ 3,00. Qual foi o valor pago por Tiago pelos 5 pacotes de bolacha?
Para resolver o problema, basta organizar o algoritmo da multiplicação:
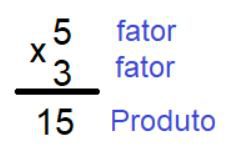
Logo, o valor pago por Tiago pelos 5 pacotes de bolacha foi: R$ 15,00
Exemplo 4. Divisão – Maria Augusta deseja dividir igualmente entre os seus três filhos a quantia de R$ 36,00. Quanto receberá cada um de seus filhos?
Para resolver esse problema, utiliza-se o algoritmo da divisão, também conhecido como divisão euclidiana.
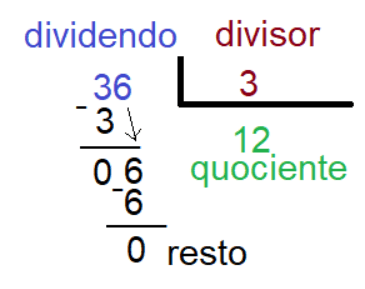
Logo, cada um dos filhos de Maria Augusta, receberá o valor de R$ 12,00.
Exemplo 5. Potência – Em uma cômoda há três gavetas, cada gaveta contém três pastas e cada pasta, contém três documentos. Quantos documentos ao todo estão nesta cômoda?
Para resolver essa situação, basta escrever o problema em forma de potência:
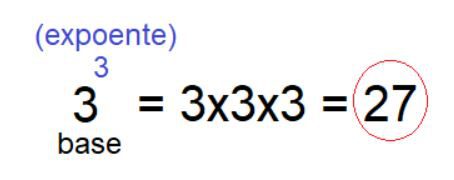
Assim, nesta cômoda há ao todo 27 documentos.
Toda potência necessita de uma base (número maior) e um expoente (número menor). O expoente determina quantas vezes a base deve multiplicar por ela mesma.
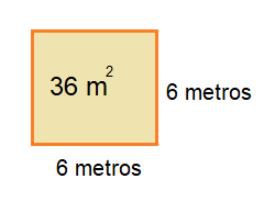
Exemplo 6. Radiciação – Sabe-se que a área de um quadrado é 36 metros quadrados. Assim, determine a medida de cada um desses lados.
Os problemas que envolvem quadrados que disponibilizam o valor da área e necessitam que você calcule o valor do lado indicam situações problemas com raíz quadrada.

Logo, a medida de cada um dos lados desse quadrado é 6 metros.
Agora que você já está expert em operações matemáticas, destaca-se os conceitos de divisores e múltiplos.
Mas, o que é um divisor de um número natural?
- Os divisores de um número natural, são aqueles números que o dividem sobrando, necessariamente, resto zero.
- Os divisores de um número natural são finitos;
- O número 1 é o menor divisor de qualquer número natural.
Por exemplo:
Os divisores de 8, são finitos, pois somente os números {1,2,4 e 8} são números que dividem o 8 restando, na divisão, resto zero.
Observe:
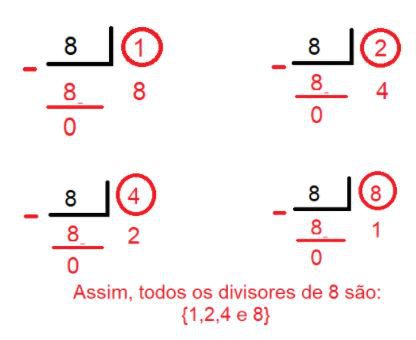
Assim, os números que são divisores do 8, são apenas quatro: {1,2,4 e 8}
Você pode determinar os divisores de um número natural por meio de diversas tentativas, ou, pode utilizar o processo de fatoração para determinar todos os divisores. Tome como exemplo, o número 100. Trata-se de um número grande, e, que, se fossemos realizar tentativas para descobrir quais seriam todos os seus divisores, provavelmente, gastaríamos um tempo consideravelmente grande. Para determinar os divisores de um número muito grande, utilizaremos o processo de fatoração.
Observe atentamente cada um dos passos, à serem seguidos:
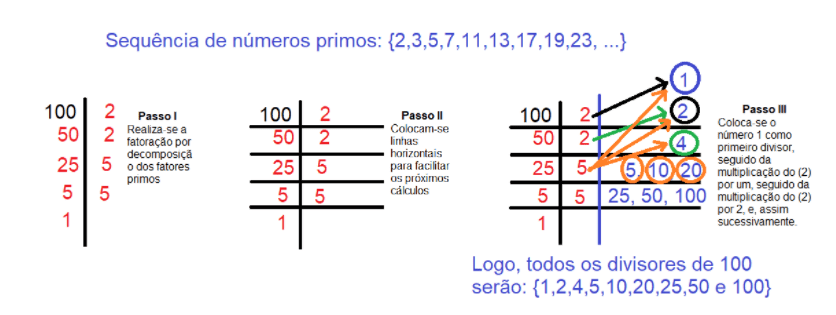
Como saber se um número divide ou não por outro? Para isso utiliza-se os critérios de divisibilidade:
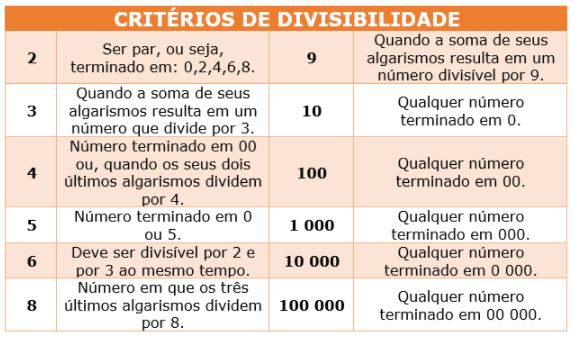
Assim, chegou a sua vez de por em prática o que você aprendeu sobre os critérios de divisibilidade, resolvendo a questão 01.
Questão 01 – Circule de vermelho todos os números que dividem por 2 e de verde todos que dividem por 3. Em seguida informe, quais desses números são divisíveis por 6.
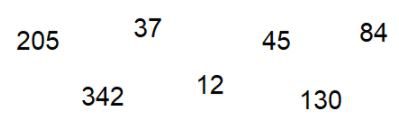
Desse modo, observe o exemplo que trata de uma situação que envolve os divisores de um número natural.
Exemplo: Dona Maria tem cortes de papel de 30 centímetros e de 20 centímetros, conforme mostra a imagem:

Ela deseja fazer cartões menores com esses dois formatos de papel, com a necessidade de fazer o maior corte possível sem que sobre restos de papel. Qual deve ser, nessas condições, o maior tamanho possível do tamanho dos cartões?
Para resolver o problema, devemos listar todos os divisores de 30 centímetros e de 20 centímetros:

Após listar todos os divisores de 30 e 20 centímetros, tem-se todas as possibilidades de corte que podem ser realizadas com os tamanhos de papel que possui Dona Maria. Mas, atendendo aos seus critérios, deve ser o maior tamanho possível!
Assim, devemos perceber quais são os divisores comuns de 30 e 20, reconhecendo o maior possível, veja:

Rapidamente, percebe-se que o maior divisor comum de 30 e 20 é 10 centímetros.
Assim, Dona Maria deverá fazer cortes de 10 centímetros para que seus cartões sejam os maiores possíveis e não haja desperdício de papel.
Muito bem! Continuando os estudos, você vai entender agora, o que são múltiplos de um número natural.
Os múltiplos de um número natural são os números obtidos da multiplicação pelos números naturais, exemplos:

Algumas considerações importantes:
Os múltiplos de um número natural são infinitos;
O zero é múltiplo de todo e qualquer número natural;
Veja uma situação que envolve o conceito de múltiplos de um número natural.
Exemplo: Um ônibus que faz a linha até o bairro Alegria parte a cada 10 minutos e o ônibus que faz a linha até o bairro Feliz parte a cada 15 minutos. Sabendo que os dois saíram juntos às 9 horas da manhã, qual será o outro horário em que eles sairão juntos novamente?
Para resolver essa situação basta listar os primeiros multiplos de 10 (bairro Alegria) e os múltiplos de 15 (bairro Feliz):

Agora basta observar qual é o primeiro múltiplo comum (com exceção do zero), dos múltiplos de 10 e 15.

Logo os dois ônibus irão sair juntos novamente em um tempo de 30 minutos,
Assim, se eles saíram juntos as 9:00 horas da manhã, basta acrescentar mais 30 minutos, ou seja, os dois ônibus sairão novamente juntos às 09 horas e 30 minutos.
Esse conceito utilizado no problema refere-se ao MMC (Mínimo Múltiplo Comum) de dois ou mais números.
Agora é com você! Continue resolvendo as questões a seguir:
Questão 02. Em uma cantina há dois tipos de suco: laranja e uva. E três tipos de lanche: pão com presunto e queijo, hamburguer e hotdog. De quantos modos diferentes pode-se combinar uma bebida de um lanche? (Use o conceito de multiplicação)
Questão 03. Marta ganhou um tabuleiro enorme com pedaços de bolo. Ao todo havia 56 pedaços para dividir igualmente com todos que moram em sua casa. Se na casa de Marta moram 8 pessoas incluindo ela, quantos pedaços de bolo cada morador deverá receber?
Questão 04. Sr. Francisco trabalha com marcenaria e deseja fazer recortes de madeira no maior tamanho possível e todos iguais para produzir uma peça. Sabe-se que o Sr. Francisco comprou dois tipos de madeira, com tamanhos de 50 centímetros e outro de 60 centímetros. Dessa maneira, atendendo todos os critérios estabelecidos, qual deve ser o maior tamanho dos cortes de madeira de modo que não tenha nenhum tipo de desperdício no material?
Questão 05. Um ônibus que faz a linha até o bairro Sudoeste parte a cada 15 minutos e o ônibus que faz a linha até o bairro Norte parte a cada 25 minutos. Sabendo que os dois saíram juntos às 9 horas da manhã, qual será o outro horário em que eles sairão juntos novamente?
RELEMBRANDO!!!!
Em síntese, nesta atividade você teve a oportunidade de estudar e compreender as operações de matemática básica, que são: adição, subtração, multiplicação, divisão, potenciação e radiciação, além de estudar os conceitos de divisores e múltiplos de um número natural, ampliando esses conceitos para o desenvolvimento do cálculo do Mínimo Múltiplo Comum e Máximo Divisor Comum.
Você finalizou a atividade de matemática de hoje! Aguardamos você até a próxima! Bons estudos!
| Ciclo da adolescência Habilidades | Habilidades Estruturantes (EF06MA05-C) Estabelecer, por meio de investigações, os critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100, 1.000, 10.000 e 100.000. (EF06MA06-B) Estabelecer e construir estratégias para determinar o Mínimo Múltiplo Comum entre pelo menos dois números naturais. (EF06MA06-D) Estabelecer estratégias para determinar o Máximo Divisor Comum entre pelo menos dois números naturais Habilidades Complementares EF06MA06-A EF06MA06-C EF06MA06-E |
