Matemática – Números, geometria e probabilidade e estatística: dividir para compartilhar um pedaço com o outro.

Olá, educando (a)! Está videoaula de Matemática foi veiculada na TV no dia 28 de Maio de 2021 (Sexta-Feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.

Nesta aula de matemática hoje, vamos compreender um pouco mais sobre frações e números racionais. Eu tenho certeza que você sabe o que é fração, afinal, quem nunca dividiu um pedaço de lanche, um chocolate, uma pizza, um bolo.

Assista a videoaula abaixo, com a temática – Matemática – Números, Geometria e Probabilidade e estatística: Dividir para compartilhar um pedaço com o outro.

AGRUPAMENTO E | 5º ANO | CICLO DA INFÂNCIA |MATEMÁTICA| PROF.ª: JUSSARA.

Dividir para compartilhar um pedaço com o outro.

Números racionais , são números que podemos escrever em forma de fração. Nesta época de pandemia, o que mais temos feito é dividir alguma coisa com alguém, não é mesmo? Afinal, muitas pessoas estão precisando de ajuda e contam com a nossa solidariedade. Então, vem comigo decifrar um pouco mais sobre estas divisões, estas partilhas numéricas e compreender como é este processo?

Disponível em: <https://pixabay.com/>. Acesso em 18 de abril de 2021.

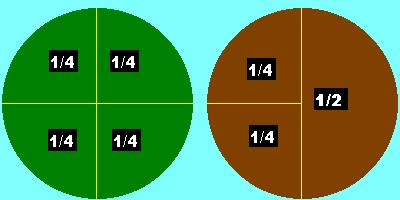
Em matemática, as partes iguais de um conjunto são conhecidas como frações. A palavra fração vem do latim frangere, que significa “quebrar”. Uma fração é chamada de fração comum quando os números (ou termos) são escritos um sobre o outro, separados por uma barra ou linha, por exemplo: 1/3 ou 3/4. Mas, você entendeu o que é uma fração? Eu digo para você que fração é a representação de uma divisão em partes iguais, ou seja, é a representação de uma parte de algo inteiro. Você deve estar pensando: Que “inteiro” professora Jussarinha?

Inteiro é o todo, aquilo que vai ser dividido. Pensem em uma maçã inteirinha ainda, sem ser partida. Nesse caso, ela é o inteiro. O total pode ser dividido em partes. O traço representa a divisão. A parte debaixo do traço se chama denominador! Ele representa em quantas partes foi dividido o inteiro. Já o número de cima se chama numerador. Ele representa a quantidade de partes iguais que foi dividido o inteiro e quais partes foram consideradas, as que foram usadas, ou comidas. As frações também são utilizadas para representar porcentagens e números decimais. O mais importante é entender que na divisão do todo, as partes devem ser iguais.

Fração

Disponível em: <https://commons.wikimedia.org/wiki/File:Fra%C3%A7%C3%B5es.png>. Acesso em 20 de Maio de 2021.

Fonte: Giovanni Junior, José Ruy – A conquista da matemática, 5º ano: componente curricular matemática: ensino fundamental, anos iniciais / José Ruy Giovanni Junior.- 1ª ed.- São Paulo: FTD, 2018

Veja que o comprimento da peça verde-escura é igual ao comprimento de 2 peças verde-claras. Então podemos dizer que o comprimento de cada peça verde-clara é igual à metade(½) do comprimento da peça verde-escura. Agora, vamos observar nesta imagem:

O comprimento da corda é igual ao comprimento de 4 palitos. Então podemos dizer que, o comprimento desse palito é igual a um quarto do comprimento dessa corda. Segundo Giovanni Júnior, para fazer as comparações entre os comprimentos, como nas duas situações apresentadas, podemos usar frações.

Consideramos a figura de um quadrado, que representa a unidade. Temos várias maneiras de dividir esse quadrado ao meio, em 2 partes iguais, cada parte representa a metade ou um meio da figura e representamos cada uma dessas partes pela fração 1/2. Se dividimos em 3 partes iguais, cada parte representa a terça parte ou um terço da figura e representamos pela fração ⅓. Mas, se dividirmos em 4 partes iguais, cada parte representa a quarta parte ou um quarto da figura, como vimos aqui.

Numerador e denominador: Numa fração, o número acima da linha é chamado de numerador. Ele indica quantas partes do todo estão sendo divididas. O número embaixo da linha é chamado de denominador. Ele indica o número total de partes que formam o conjunto.

Para ler uma fração comum, comece pelo numerador. Leia o numerador na forma cardinal e o denominador na forma ordinal. Por exemplo, 3/4 lê-se como “três quartos”. No caso de denominadores maiores que 10, o denominador é lido na forma cardinal, acompanhado da palavra avos. Por exemplo, a fração 5/12 é lida como “cinco doze avos”.

Leitura de fração:

Tipos de fração

Os três tipos mais simples de frações comuns são: própria, imprópria e mista. Em uma fração própria, o numerador é menor do que o denominador. Vejamos a situação problema, onde um menino ganhou 2 cartelas com 4 figurinhas em cada uma, e a maneira de representar a quantidade de cartelas que ele ganhou é 2 ¼ 2 inteiros e 1 quarto.

A fração formada é chamada de número misto, porque é formada por uma parte inteira e por uma parte fracionária. Assim, a parte inteira é o 2 e a fracionária é ¼. As frações chamadas de próprias, São aquelas que possuem o numerador menor que o denominador. Já as frações impróprias são aquelas que possuem o numerador maior ou igual ao denominador.

Preste atenção: Hoje estamos falando dos números naturais que são aqueles que podemos literalmente contar tudo com eles. São representados pela letra N= {0,1,2,3,4,..10}. Falamos dos números inteiros e o seu negativo, ou seja, é o número natural e sua versão negativa. É representado pela letra Z= {-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}. Estamos dando uma atenção especial para os números racionais, os fracionários. Eles são representados pela letra Q={4/2=2,5/3=1,6 ,5/1=5}.

Relembrando a aula: Então moçada, nesta aula de matemática, falamos sobre as frações e os números que podem ser escrito desta forma, além de alguns tipos de fração, sua leitura e aprendemos o que é um numerador e um denominador e seu papel numa fração. Pra não perder o costume, vamos à nossa atividade, na verdade um desafio gastronômico.

Atividade

Questão 1 – Com a ajuda de um adulto, faça um bolo, bem simples, depois divida-o em pedaços do mesmo tamanho. Distribua para as pessoas que estiverem próximas a você, observe se tem alguém aí por perto da sua casa que esteja precisando de alimentação e seja solidário em doar. Anote no seu caderno quantos pedaços você conseguiu dividir a forma de bolo. Veja a receita: Ingredientes:

200 gramas de manteiga

1 e 1/2 xícara (de chá) de açúcar

4 ovos

3 xícaras (de chá) de farinha de trigo

1/2 xícara (de chá) de leite

1 colher (de sopa) de fermento para bolo

Modo de Preparo:

Coloque tudo aos poucos em uma tigela e bata bem até o creme ficar fofo e esbranquiçado. Bata por uns 5 minutos. Despeje a massa na forma untada e polvilhada. Coloque no forno preaquecido e não abra o forno nos primeiros 30 minutos. Ele deve assar entre 35 e 45 minutos. Seu bolo vai estar bom quando você enfiar um palito nele e ele sair limpo.

Questão 2 – Observe as divisões das figuras, copie em seu caderno, representando a fração imprópria e o número misto:

Beijos da Professora Jussarinha pra todos vocês. Tchauzinho pessoal.

Habilidade estruturante:

(EF05MA02-B) Comparar e ordenar números racionais de uso frequente, nas representações fracionária e decimal e representá-los na reta numérica.
(EF05MA02-A) Reconhecer os termos da fração e fazer leitura de números racionais de uso frequente, nas representações fracionária e decimal, e representá-los na reta numérica.
(EF05MA03-B) Identificar e representar frações (igual, menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando materiais manipuláveis e/ou não a reta numérica, como recursos
(EF05MA03-A) Reconhecer os significados dos números racionais, parte/todo, quociente, e utilizá-los em diferentes contextos.

Referências:

Giovanni Junior, José Ruy – A conquista da matemática, 5º ano: componente curricular matemática: ensino fundamental, anos iniciais / José Ruy Giovanni Junior.- 1ª ed.- São Paulo: FTD, 2018.
Frações. 1 fot., color. In Britannica Escola. Web, 2021. Disponível em: <https://escola.britannica.com.br/artigo/frações/603332/recursos/238891>. Acesso em: 27 de maio de 2021.