Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAF_gnPjsYY/vTem8qEIWZw5uo9oeuW4CA/edit?utm_content=DAF_gnPjsYY&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 14 de março de 2024.
A álgebra é uma linguagem muito útil na matemática que nos permite modelar e resolver uma variedade de problemas do mundo real. Nesse contexto estão as expressões algébricas, que são compostas por termos matemáticos chamados monômios. Neste texto, exploraremos a importância de reconhecer e compreender expressões algébricas, focando especialmente nos monômios e suas operações. Além disso, discutiremos como resolver exercícios relacionados a esse assunto.
Importância da Compreensão de Expressões Algébricas:
A habilidade de reconhecer e compreender expressões algébricas é fundamental em várias áreas, incluindo ciências, engenharia, economia e computação. Essas expressões nos permitem formular modelos matemáticos para entender e resolver uma ampla gama de problemas.
Monômios:
Um monômio é uma expressão algébrica que consiste em um único termo. Ele pode ser representado por uma constante, uma variável elevada a uma potência ou o produto de uma constante e uma ou mais variáveis elevadas a potências. Por exemplo, 2x, 3xy2, e 4 são monômios.
Elementos de Monômios:
Os monômios têm dois elementos principais: o coeficiente e a parte literal. O coeficiente é o número multiplicado pela parte literal e pode ser positivo, negativo ou zero. Na expressão 3xy2, o coeficiente é 3. A parte literal é a parte que contém as variáveis elevadas a potências. Na mesma expressão, a parte literal é xy2.
Operações entre Monômios:
Existem três operações básicas entre monômios: adição, subtração e multiplicação.
Adição e Subtração: Para adicionar ou subtrair monômios, é essencial que as partes literais sejam idênticas. Os coeficientes são simplesmente somados ou subtraídos enquanto as partes literais permanecem as mesmas. Por exemplo:
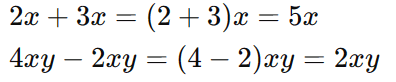
Multiplicação: Na multiplicação de monômios, os coeficientes são multiplicados entre si e as partes literais são combinadas pela regra dos expoentes. Por exemplo:
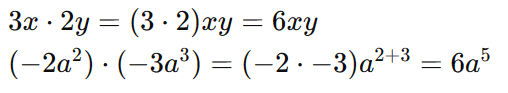
Resolvendo Exercícios sobre Monômios:
Maria está estudando para uma competição de matemática e está revisando adição de monômios. Ela tem os seguintes monômios:
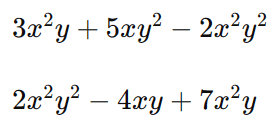
Ela quer somar esses monômios para simplificar a expressão. Ajude Maria a encontrar a soma simplificada.
Resolução:
Para resolver esse problema, vamos primeiro agrupar os monômios com termos semelhantes e depois adicionar os coeficientes.
Os monômios são:
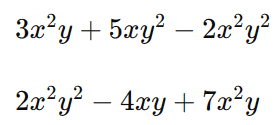
Agora, agrupando os termos semelhantes, temos:
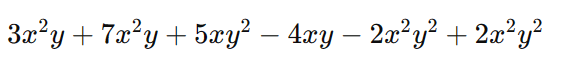
Agora, podemos adicionar os coeficientes de termos semelhantes:
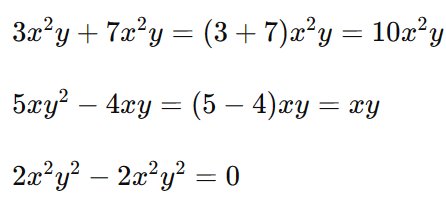
Portanto, a expressão simplificada é:
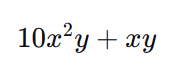
QUESTÃO 1
Uma empresa fabrica um produto cujo preço de venda é dado pelo polinômio 4x2+3x+6, onde x é o número de unidades vendidas. O custo de produção é representado pelo polinômio 2x2+2x+4. Sabendo que o lucro é calculado subtraindo o preço de venda pelo preço de custo, então o lucro do produto é
(A) 2x2 – x + 4
(B) 2x2 + x + 10
(C) 2x2 + x + 4
(D) 2x2 + x + 2
QUESTÃO 2
Uma loja vende um produto por um preço representado pelo polinômio 3x2+2x+5, onde x representa a quantidade de unidades vendidas. O custo de produção desse produto é representado pelo polinômio 2x2+4x+3. O lucro total da loja ao vender esse produto é
(A) 21x + 2
(B) x2 + 6x + 2
(C) x2 − 2x + 2
(D) x2 − 2x − 2
QUESTÃO 3
Uma fábrica produz camisetas e bonés. O custo de produção diário das camisetas é representado por 3x+2y reais, onde x é o custo do algodão utilizado e y é o custo de mão de obra empregada. O custo de produção diário de bonés é representado por 2x+4y reais. Então, qual o custo total diário da fabricação de camisetas e bonés?
QUESTÃO 4
João está praticando para uma competição de matemática e encontrou as seguintes expressões:
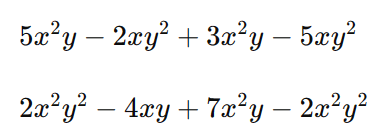
Ele quer calcular a soma dessas duas expressões. Faça esses cálculos para ver qual resultado ele deve encontrar.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF08MA06-A) Reconhecer e compreender uma expressão algébrica, destacando dentre elas os monômios e polinômios, bem como os seus elementos como coeficientes e partes literais. (EF08MA06-B) Identificar monômios e polinômios (binômio, trinômio, entre outros) com os seus respectivos graus, coeficientes e partes literais. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 11/03/2024. |

