Esta atividade de Matemática, tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 6º ano do Ensino Fundamental.

Disponível em: < a href=’https://br.freepik.com/fotos-vetores-gratis/relogio’>Relógio vetor criado por freepik – br.freepik.com</a> Acesso em 12, Abril 22.
As unidades de medida desempenham um papel fundamental na comunicação eficaz e na compreensão universal das quantidades. A padronização dessas unidades é essencial para garantir consistência e precisão em diversas áreas, desde a ciência e a tecnologia até o comércio e a vida cotidiana. A adoção de unidades padronizadas cria uma linguagem comum que facilita a troca de informações em todo o mundo.
Unidades de Medida de Comprimento
Ao abordar a medida de comprimento, destacamos a importância de uma unidade universal que possa ser compreendida globalmente. O Sistema Internacional de Unidades (SI) estabeleceu o metro como a unidade padrão para comprimento. Veja outras unidades de medida derivadas do metro:
1 quilômetro = 1000 metros
1 km = 1000 m
1 metro = 100 centímetros
1 m = 100 cm
1 centímetro = 10 milímetros
1 cm = 10 mm
Unidades de Medida de Massa
No contexto da massa, a padronização é importante para garantir a precisão nas medições. O quilograma, definido pelo SI como a unidade padrão de massa, serve como referência para pesagens em laboratórios, indústrias e comércio. A estabilidade dessa unidade é essencial para garantir que as medições de massa permaneçam confiáveis e consistentes ao longo do tempo. Veja algumas relações entre unidades de medida de massa:
1 quilograma = 1000 gramas
1kg = 1000 g
1 tonelada = 1000 quilogramas
1 t = 1000 kg
Unidades de Medida de Capacidade
A medição de capacidade é vital em atividades diárias, como culinária, indústria de alimentos e química. O litro, uma unidade do SI, é amplamente utilizado para medir volume e capacidade. A padronização do litro facilita a comparação de quantidades líquidas em diferentes contextos, proporcionando eficiência e clareza em diversas aplicações.
1 litro = 1000 mililitros
1L = 1000 mL
Unidades de Medida de Tempo
O tempo é uma medida importante em diversas áreas, desde a cronologia histórica até as operações precisas da tecnologia moderna. O segundo, definido pelo SI, é a unidade padrão para medir o tempo. A padronização do segundo é fundamental para sincronizar processos globais, como a comunicação entre satélites, a navegação por GPS e as transações financeiras. Veja que:
1hora = 60 minutos
1minuto = 60 segundos
Em resumo, as unidades de medida padronizadas são como “regrinhas” que todos usam para medir as coisas da mesma maneira. Isso é muito importante porque ajuda as pessoas de diferentes lugares a entenderem as quantidades da mesma forma. Imagine se cada pessoa usasse uma regra diferente para medir o comprimento, o peso, a quantidade de líquido ou o tempo. Seria confuso, não é? Com as unidades padronizadas, todos usam as mesmas “regrinhas”, o que facilita muito a comunicação e o entendimento entre as pessoas em todo o mundo. Isso é útil em muitas áreas, como na ciência, no comércio e até mesmo na cozinha!
Assista a videoula abaixo da professora Priscilla com essa temática.
Sabendo isso, responda a atividade abaixo:
Questão 1
Uma sala com formato retangular tem 500 cm de largura e 600 cm de comprimento. Responda:
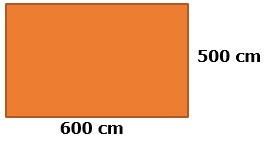
Imagem do arquivo pessoal
- Qual o perímetro dessa sala em centímetros?
- E em metros?
- Qual a área dessa sala em metros quadrados?
Questão 2
No dia 23 de abril Daniela fará um curso profissionalizante. O curso começará às 19:00 e serão quatro aulas com duração de 45 minutos e um intervalo de 15 minutos. Responda:
- Qual é o horário de encerramento do curso?
- Ao observar a data do curso, Daniela percebeu que seu aniversário é exatamente depois de duas semanas. Qual é o dia do aniversário de Daniela?
Questão 3
No dia 27 de março de 2022, a temperatura máxima prevista para Goiânia foi de 32º e mínima de 21º. Então qual foi a variação de temperatura nesse dia?
(A) A variação de temperatura foi de 9º.
(B) A variação de temperatura foi de 11º.
(C) A variação de temperatura foi de 20º
(D) A variação de temperatura foi de 15º.
Questão 4
Em uma receita de bolinho sem farinha são necessárias 400 gramas de aveia. Quantos quilogramas de aveia serão necessários para fazer 5 receitas como essa?
(A) Serão necessários 4 quilogramas de aveia.
(B) Serão necessários 2 quilogramas de aveia.
(C) Serão necessários 2,5 quilogramas de aveia.
(D) Serão necessários 5 quilogramas de aveia.
Questão 5
Calcula-se que em uma festa cada convidado consome cerca de 600 mL de refrigerante. Para uma festa com 60 convidados, quantos litros de refrigerante serão necessários? Quantas garrafas de 2 litros de refrigerante deverão ser compradas?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidade: | (EF05MA19-A) Ler, interpretar, resolver e elaborar problemas envolvendo medidas de comprimento, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais. (EF05MA19-B) Ler, interpretar, resolver e elaborar problemas envolvendo medidas de área, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais. (EF05MA19-C) Ler, interpretar, resolver e elaborar problemas envolvendo medidas de massa, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais. (EF05MA19-D) Ler, interpretar, resolver e elaborar problemas envolvendo medidas de tempo, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais. (EF05MA19-E) Ler, interpretar, resolver e elaborar problemas envolvendo medidas de temperatura, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais. (EF05MA19-F) Ler, interpretar, resolver e elaborar problemas envolvendo medidas de capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais utilizando gráficos e tabelas. (EF05MA19-G) Reconhecer as medidas de área e de perímetro de figuras planas na malha quadriculada. (EF05MA21) Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos. (EF06MA24) Ler, interpretar, resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender sempre. 6°. Ano – Ensino Fundamental; Língua Portuguesa e Matemática; 2°. Bimestre; Goiânia, 2022. |
