Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6º Ano do Ensino Fundamental – Anos Finais.
MÁXIMO DIVISOR COMUM
O máximo divisor comum, abreviado por M.D.C., é o maior número natural possível, que divide simultaneamente, dois ou mais números naturais de forma exata. Aqui vale relembrar o conceito de divisor.

Por exemplo: 4 é divisor de 20, porque 20 dividido por 4 tem resto zero.
Um número natural pode ter vários divisores. Veja um exemplo: os divisores de 20 são
D(20) = (1, 2, 4, 5, 10, 20)
A divisão de 20 por qualquer dos seus divisores é exata.
Os números naturais podem ter divisores comuns. Vejamos quais são os divisores de 24.
D(24) = (1, 2, 3, 4, 6, 12, 24)
Observe que 20 e 24 têm como divisores em comum
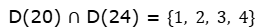
Logo, o máximo divisor comum entre 20 e 24 é o número 4.
Em linguagem matemática, M.D.C. (20, 24) = 4.
O algoritmo de Euclides
Um método simples para calcular o M.D.C. entre dois números é o algoritmo de Euclides. Este método usa de divisões sucessivas para determinar o divisor comum, ou seja, até chegar ao resto zero. As divisões são feitas numa grade como esta da imagem
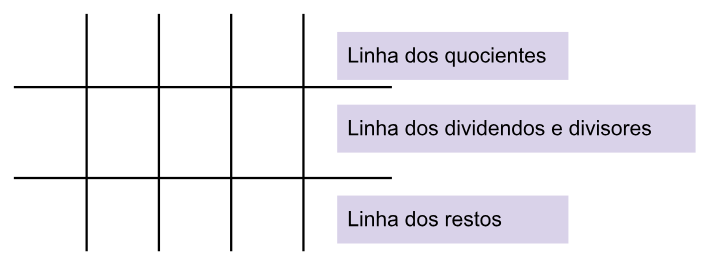
Imagem 1: Algoritmo de Euclides – divisões sucessivas – Acervo NEC.
Vamos calcular o M.D.C. (20, 24) pelo método de divisões sucessivas.
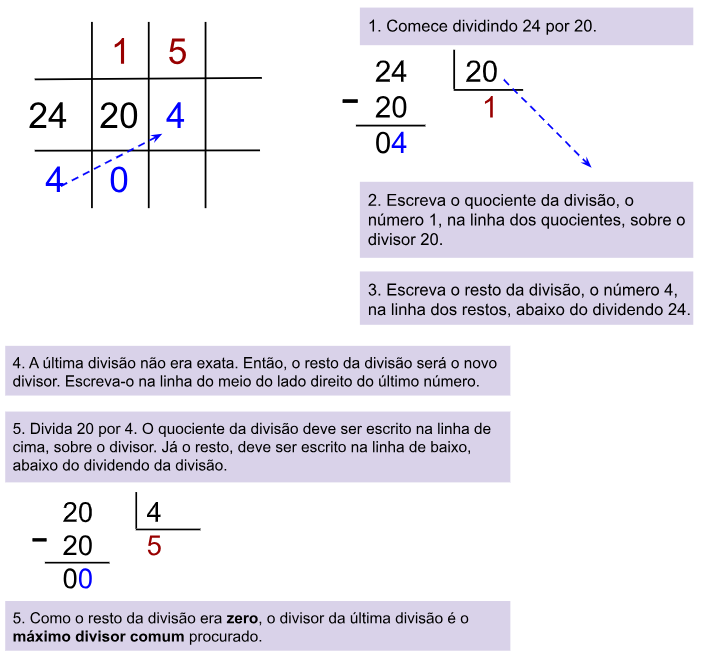
Logo, o M.D.C.(20, 24) = 4.
Agora é a sua vez de calcular o M.D. C.. Escolha um método e mãos à obra. Bom estudo!
QUESTÃO 1
Para a comemoração do “dia do estudante”, a turma do 6º ano vai montar kits com a mesma quantidade de guloseimas, entre doces e biscoitos. A turma arrecadou 60 doces e 36 biscoitos para montar o maior número de kits possível, sem que sobre nenhum doce ou biscoito. Com essas guloseimas, a turma conseguiu montar
(A) 6 kits.
(B) 9 kits.
(C) 10 kits.
(D) 12 kits.
QUESTÃO 2
Abaixo há uma tabela com os divisores de alguns números naturais.
| Nº | Divisores | ||||||||
| 15 | 1 | 3 | 5 | 15 | |||||
| 18 | 1 | 2 | 3 | 6 | 9 | 18 | |||
| 20 | 1 | 2 | 4 | 5 | 10 | 20 | |||
| 24 | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 | |
| 36 | 1 | 2 | 3 | 4 | 6 | 9 | 12 | 18 | 36 |
Com base nessa tabela, responda às perguntas a seguir:
A) Quais são os divisores comuns entre 18 e 24?
B) Qual é o M.D.C.(15, 20)?
C) Qual número da tabela tem a maior quantidade de divisores?
QUESTÃO 3
No jogo de tabuleiro “Qual é o Divisor?”, cada jogador retira uma carta com uma pergunta. Se responder corretamente, avança uma casa. Na última rodada, Enzo pegou uma carta com a seguinte pergunta:
“Sou o maior divisor comum de 45 e 75. Que número sou eu?”
Enzo acertou a pergunta respondendo
(A) 15.
(B) 10.
(C) 5.
(D) 1.
QUESTÃO 4
Para calcular o M.D.C.(28, 48), Pedro usou o método de divisões sucessivas, mas não concluiu. Com base no que já está na figura abaixo, continue o cálculo e determine o máximo divisor comum entre esses números.
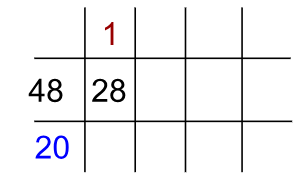
SAIBA MAIS
Quer aprender ou rever o conceito de máximo divisor comum e o método de divisões sucessivas, também conhecido como algoritmo de Euclides, assista a animação “M.D.C. pelo método de divisões sucessivas”, do canal da professora Cristiane Souza, no YouTube.
Vídeo 1: MDC pelo método de divisões sucessivas – Canal Professora Cristiane Souza, YouTube.
| Autoria | Cristiane Soares de Souza, licenciatura em Matemática. |
| Componente Curricular | Matemática |
| Habilidades | (EF06MA06-C) Reconhecer e compreender o Máximo Divisor Comum entre pelo menos dois números naturais. (EF06MA06-D) Estabelecer estratégias para determinar o Máximo Divisor Comum entre pelo menos dois números naturais. (EF06MA06-E) Ler, interpretar, elaborar e resolver problemas que envolvam as ideias de múltiplo e de divisor, por meio de desafios matemáticos contextualizados. |
| Referências | BARBOSA, Gabriela S. Encenando os múltiplos e os divisores. VIII Encontro de Educação Matemática, Universidade Gama Filho, FEUC. 2004. Disponível na URL https://www.sbembrasil.org.br/files/viii/pdf/09/RE05246478793.pdf , consultado em 04/11/2024. VALENTIM, Erivan Sousa. A divisibilidade no Ensino Fundamental. Dissertação Programa de Pós-graduação Profissional em Matemática – PROFMAT, Universidade Estadual da Paraíba, Campina Grande, 2017. Disponível na URL https://tede.bc.uepb.edu.br/jspui/handle/tede/2828 , consultado em 04/11/2024. |

