Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Disponível em: <https://www.canva.com/design/DAGFObHD9EU/qCpUtuLx0_wlpjG1FIkrhQ/edit?utm_content=DAGFObHD9EU&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
A notação científica é uma forma de representar números muito grandes ou muito pequenos de maneira mais compacta. Dessa forma facilitando cálculos, comparações e interpretações em situações práticas e científicas. Ela permite lidar com números que podem ser impraticáveis de se escrever ou manipular em sua forma decimal padrão. Ela é utilizada em diversas áreas da ciência, engenharia, matemática e outras disciplinas.
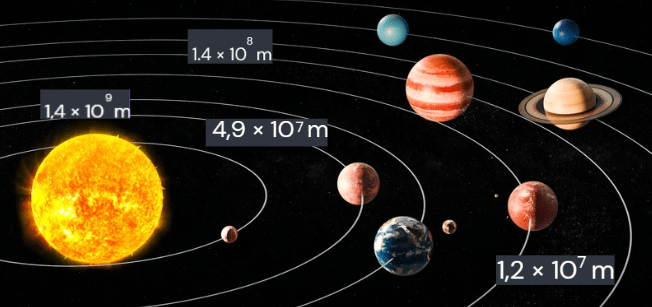
Um exemplo da importância da notação científica está na astronomia. Distâncias astronômicas, como as entre planetas, estrelas e galáxias, são enormes e são frequentemente expressas em notação científica para simplificação. Da mesma forma, a física de partículas lida com números muito pequenos, como massas de elétrons e distâncias atômicas, que são mais facilmente manuseáveis em notação científica.
Vamos agora explorar alguns exemplos resolvidos de exercícios envolvendo notação científica e diferentes operações matemáticas:
Adição e Subtração: Para somar ou subtrair números escritos na notação científica, é necessário que os expoentes sejam iguais, veja:
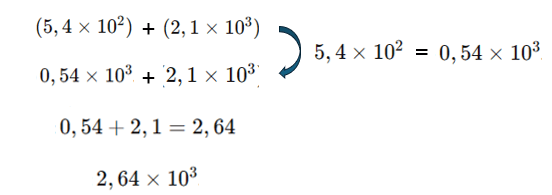
Multiplicação: Multiplicamos os números decimais, e usamos as propriedades de potências:
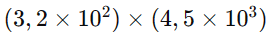
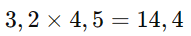
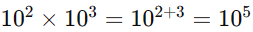
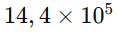
Divisão: Dividimos os números decimais, e usamos as propriedades de potências:
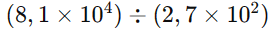
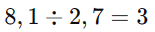
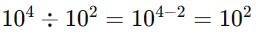
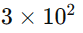
Potenciação: Usamos as propriedades da potenciação.
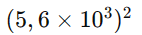
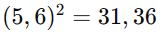
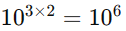
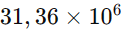
Agora que você , que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
A distância entre duas cidades é de 120.000 metros. Esse número em notação científica corresponde a

QUESTÃO 2
O diâmetro de uma célula é de 2×10−6 metros. Se colocarmos 100 dessas células lado a lado, o comprimento total será
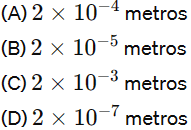
QUESTÃO 3
Um terremoto teve uma magnitude de 6,8×100. Se outro terremoto teve uma magnitude de 2,3×101, qual foi a diferença entre as magnitudes?
QUESTÃO 4
Um grama de sal contém 6,022×1023 moléculas. Se tivermos 3 gramas de sal, quantas moléculas de sal teremos?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA04-B) Ler, interpretar, resolver e elaborar problemas com números reais, inclusive em Notação Científica, envolvendo diferentes operações. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |