Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento H (8º ano)_Ciclo da adolescência foi veiculada na TV no dia 28/04/2021 (Quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 8º ano, irá estudar sobre alguns conceitos algébricos, tais como: valor numérico de expressões algébricas, monômios, polinômios, produtos notáveis, quocientes notáveis, operações envolvendo polinômios (adição, subtração, multiplicação e divisão).
Assista a videoaula a seguir com a temática: Álgebra
Olá, nesta atividade de matemática você vai estudar alguns conceitos algébricos, ressaltando:
- Valor numérico de uma expressão algébrica;
- Monômios, binômios, trinômios e polinômios;
- Produtos notáveis;
- Quociente notáveis;
- Operações de adição, subtração, multiplicação e divisão de polinômios.
Para iniciar seus estudos vale ressaltar que o trabalho com a álgebra exige-nos trabalhar com valores ou até mesmo aspectos desconhecidos, aos quais disponibilizamos as letras para representar tais valores.
Na situação abaixo, tem-se alguns itens de supermercado, os quais estão “ocultos” desconhecidos os seus valores de custo. Observe:

Suponha que uma pessoa vá ao supermercado e compre duas caixas de sabão em pó, um queijo e cinco pacotes de bolacha.
Qual a expressão algébrica capaz de representar essas compras?
Após pensar um pouco, você terá que agrupar os termos semelhantes desta situação, levando-se em conta os valores expressos por letras nesta situação:
2 caixas de sabão em pó – com preço de x reais cada uma = 2x
1 queijo – com preço de y reais = y
5 pacotes de bolacha – com preço de z reais cada um = 5z.
Logo, a expressão algébrica que consegue demonstrar essa situação de compra será dada pela soma de todos esses itens:
2x + y + 5z
Tem-se aqui uma expressão algébrica.
Fazendo uso dessa expressão algébrica, suponha que o valor de cada caixa de sabão em pó é R$ 9,00, o valor do queijo seja R$ 15,00 e o valor de cada pacote de bolacha seja R$ 3,00.
Nessas condições substituiremos na expressão algébrica, os seus respectivos valores:
x por 9
y por 15
z por 3
Resultando em:
2.9 + 15 + 5.3
18 + 15 + 15
48
Assim, o valor destes itens terá um custo total de R$ 48,00.
Esse procedimento de substituir valores aos termos desconhecidos é chamado em matemática de valor numérico da expressão algébrica.
Dando sequência a nossos estudos, uma expressão algébrica pode ser classificada ao número de termos que possui em somas ou subtrações. No caso do exemplo anterior, percebe-se que haviam três termos.
Monômios
Para compreender o conceito de monômio, observe o retângulo abaixo:
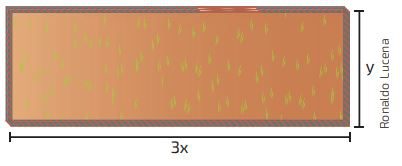
Este retângulo possui 3x de medida de comprimento e y de medida de largura. Para determinar a sua área, deve-se multiplicar o comprimento (3x) pela largura (y), resultando em:
3xy
A expressão algébrica 3xy é caracterizada como um monômio, pois apresenta um único termo.
Observe com atenção a definição de monômio:

Observe alguns outros tipos de monômios:
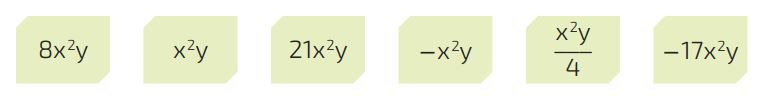
Agora que você sabe que os monômios são compostos por um único termo, que, por sua vez compõe-se de: coeficiente (número) e parte literal (letras), resolva a questão 01.
Questão 01. Abaixo, tem-se alguns exemplos de como identificar o coeficiente e a parte literal de um monômio. Com base nos exemplos citados, determine em cada um dos itens, a parte literal e o coeficiente de cada um dos monômios.

Agora que você já sabe o que é um monômio, veja como agrupar termos semelhantes de um monômio. Para isso, observe com atenção a composição dos blocos realizado por meio de três figuras.
Você seria capaz de elaborar uma expressão algébrica que representasse todo esse volume?
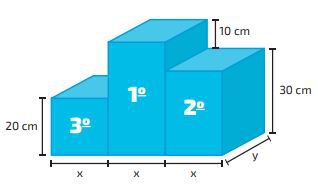
Primeiramente deve-se lembrar que o volume de um sólido geométrico, sobretudo de um bloco retangular, pode ser calculado (obtido) por meio da multiplicação do comprimento pela largura pela altura.
No entanto estes blocos apresentam tamanhos distintos, o que nos obriga a separá-los para obter êxito nos cálculos, conforme mostra a próxima imagem:
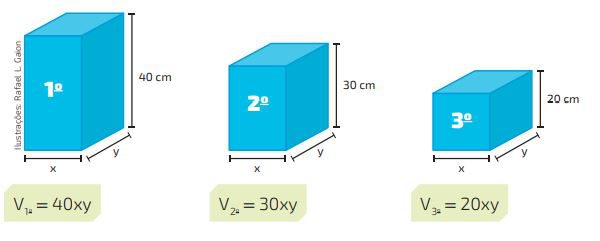
Cada um dos blocos foram separados por ordem de tamanho e já descritos o volume de cada um deles, repetindo, obtidos da multiplicação do comprimento pela largura pela altura.
Assim, para saber o volume dos blocos juntos, há a necessidade de somar o volume de cada um deles:
40xy + 30xy + 20xy
Repare que todas as partes literais dessa expressão numérica são formadas por xy, o que indica que a soma pode ser realizada, conservando a parte literal e somando os coeficientes (valores numéricos), resultando em:
40xy + 30xy + 20xy
90xy
O volume da composição dos blocos retangulares pode ser expresso pelo monômio 90xy.
Coloque em prática seus conhecimentos sobre monômios!
Questão 02. Abaixo, tem-se dois quadriláteros, um quadrado com medida de lado a e um retângulo com medidas de comprimento 2x e largura 3y. Determine a área de cada um deles, informando o monômio que cada figura representa.
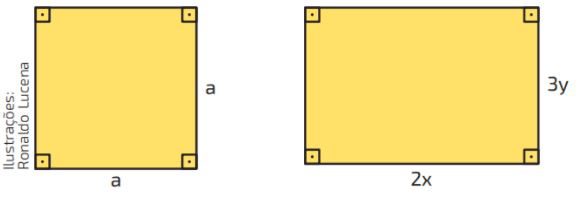
Quando se tem diferentes monômios escritos numa expressão algébrica com somas ou subtrações que não possuem a mesma parte literal, tem-se o que se denomina por polinômios.
Observe com atenção o exemplo abaixo:

Você deve ter percebido neste exemplo que os polinômios apresentam mais de um termo, e, de acordo com a quantidade de termos de um polinômio, pode-se caracterizar por nomes específicos a expressão algébrica. Acredito que seja a hora de ampliar tais conceitos!
Os polinômios
Os polinômios são expressões algébricas formadas pela adição (ou subtração) algébrica de monômios, sendo cada monômio um termo do polinômio.
Dependendo da quantidade de termos, um polinômio recebe um nome específico.
- Os polinômios que possuem um termo são chamados de monômios;
- Os polinômios que possuem dois termos são chamados de binômios;
- Os polinômios que possuem três termos são chamados de trinômios;
- Os polinômios que possuem quatro ou mais termos não recebem um nome específico.

Ampliando os estudos dos conceitos algébricos é possível perceber algumas multiplicações que são tão evidentes na álgebra que recebem o nome de produto (por ser o resultado de uma multiplicação) notáveis, ou seja, multiplicações que estão em evidência no conhecimento matemático.
Acompanhe:
Produtos notáveis
Quadrado da Soma
A expressão “quadrado da soma” dos produtos notáveis vem da multiplicação geométrica de um quadrado que necessita ser calculado a área, por isso quadrado da soma. Para entender melhor de que quadrado se trata, observe o esquema:
Iniciamos com um quadrado simples de lado a:
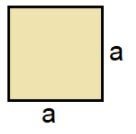
Se acrescentarmos a esse quadrado uma medida b em cada uma de suas dimensões, tem-se uma nova figura:
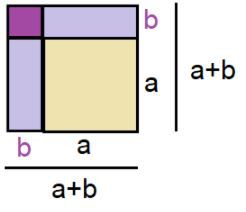
Essa nova figura, por sua vez, forma um outro quadrado maior, que tem dimensões de (a+b) por (a+b).
Para calcular a área do quadrado maior, tem-se dois caminhos: a resolução geométrica e a resolução algébrica, conforme mostra as imagens abaixo:
Resolução geométrica

Resolução algébrica
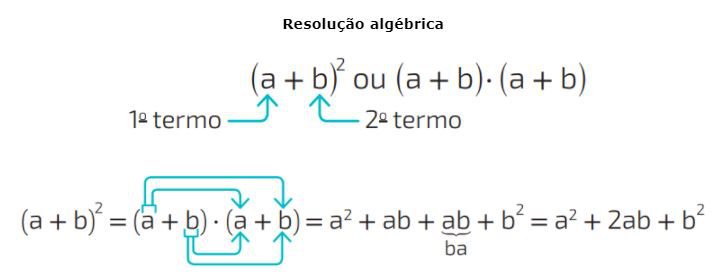
Note que na resolução algébrica os termos são multiplicados pela propriedade distributiva. Independemente de qual método utilizar, a resolução do produto notável da soma, sempre resultará em um trinômio:
a2+2ab+b2, pois ele terá três termos, ou seja, composto por três monômios.
Quadrado da Diferença
O produto notável expresso pelo quadrado da diferença incia-se com um quadrado grande, com dimensões a por a, e, desse quadrado são retiradas as partes b, restando somente o quadrado azul da imagem abaixo:
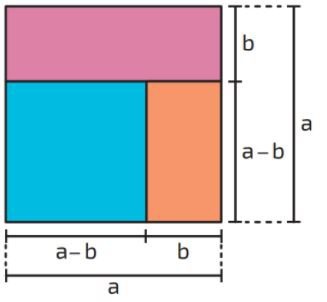
Observe que a multiplicação que se tem agora é dada pelas dimensões (a-b) por (a-b). Abaixo, tem-se a sua resolução algébrica, acompanhe:
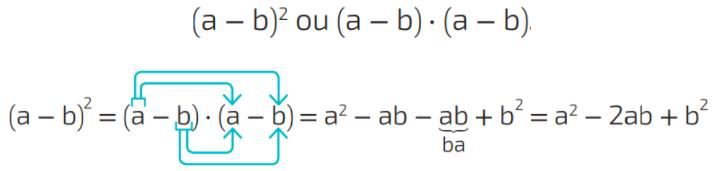
Assim o produto notável da diferença indicado pela multiplicação dos termos (a-b) por (a-b), resulta, também, em um trinômio:
a2-2ab + b2 .
Produto da soma pela diferença
O produto notável da soma pela diferença, trata de uma multiplicação que contém uma soma e uma subtração com os mesmos termos, tais como: (a+b) por (a-b). Abaixo, tem-se a sua representação geométrica e a sua resolução algébrica.
Acompanhe o passo a passo.
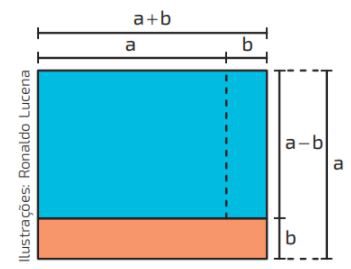
Aqui, mostra-se o esquema da multiplicação dos lados compostos por (a+b) e (a-b). A seguir tem-se a resolução algébrica desse produto notável.
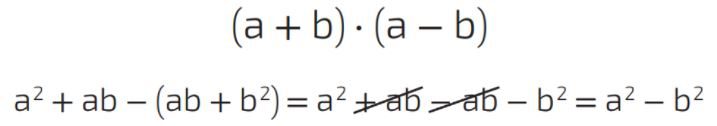
Assim o produto notável da diferença representa um binômio
a2–b2 , pois somente contém dois termos.
Agora que você conhece os produtos notáveis: da soma, da diferença e da soma pela diferença, observe a sua aplicação prática e contextual em uma situação problema:
A figura a seguir é composta de dois quadrados e dois retângulos, observe:
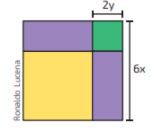
Determine o polinômio que representa a área do quadrado amarelo.
Para resolver o problema é necessário identificar as dimensões do quadrado amarelo.
Como 6x é maior que o lado do quadrado amarelo, devemos retirar dele a parte 2y, isso em cada um de seus lados, tendo:
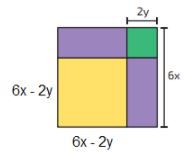
Agora, basta multiplicar (6x-2y) por (6x-2y):
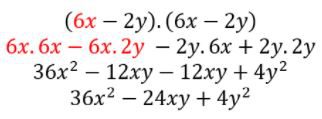
Logo a área do quadrado amarelo é obtida pelo quadrado da diferença, resultando em trinômio:
36×2 – 24xy + 4y2 .
Agora é com você! Resolva as questões:
Questão 03. Calcule a expressão algébrica capaz de determinar o perímetro das figuras abaixo:
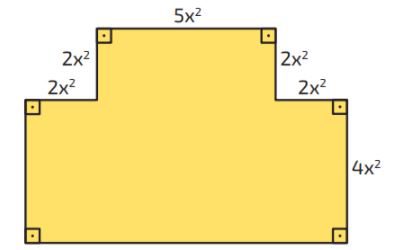
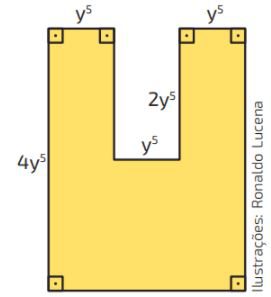
Questão 04. Calcule o valor da área de cada uma das figuras que estão em amarelo e em seguida marque qual das respostas abaixo corresponde a área indicada.
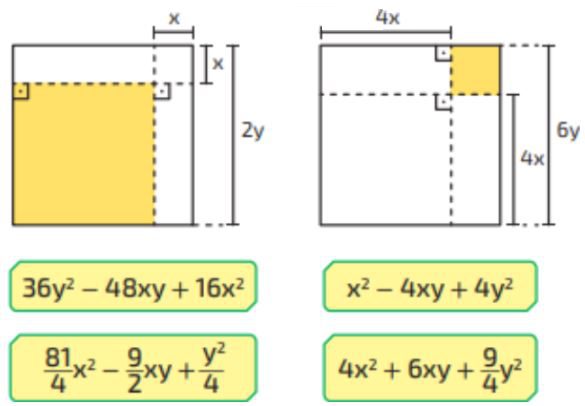
RELEMBRANDO!!!!!!!
Nesta atividade de matemática, você percebeu a utilidade do conhecimento algébrico e suas possíveis interações com a geometria, estudando com as expressões algébricas o valor numérico delas. Estudou os modos de categorizar as expressões algébricas em: monômios, binômios, trinômios e polinômios, estabelecendo algumas operações matemáticas entre eles, observando os produtos notáveis e seus processos de resolução.
Parabéns pelo estudo, continue se esforçando e com atenção às atividades do conexão escola.
Até a próxima atividade de matemática!
| Referências | DANTE, Luiz Roberto. Teláris matemática, 8º ano: ensino fundamental, anos finais – 3. ed. – São Paulo : Ática, 2018. PATARO, Patricia Moreno., BALESTRI, Rodrigo. Matemática essencial 8o ano : ensino fundamental, anos finais – 1. ed. – São Paulo : Scipione, 2018. PLND |
| Ciclo da Adolescência Habilidades | Habilidade Estruturante: (EF08MA06-D) Associar os polinômios aos modelos geométricos de figuras planas (cálculo de perímetros e áreas), aos modelos de sólidos geométricos (cálculo de áreas da base e áreas laterais em planificações, cálculo de volumes) e os modelos que surgem em diversas situações do cotidiano como o valor a se pagar numa corrida de táxi, os valores de receita, custo e lucro de uma empresa dependendo da quantidade de produtos comercializados, entre outras. Habilidades complementares: EF08MA06 AEF08MA06 BEF08MA06-C |
