Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento I (9º ano)_Ciclo da adolescência foi veiculada na TV no dia 29/04/2021 (Quita-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 9º ano, irá identificar e reconhecer as funções, representações numérica, algébrica e gráfica, funções de 1° Grau, cálculo do valor numérico de funções de 1° Grau , comportamento da função de 1° Grau.
Assista a videoaula a seguir com a temática: Álgebra e Funções
Olá estudante do nono ano da Rede Municipal de Educação da Cidade de Goiânia!
Nesta atividade de matemática você vai estudar alguns conceitos algébricos, ressaltando:
- O conceito de função polinomial do primeiro grau;
- Representações algébricas e geométricas de uma função do primeiro grau;
- Valor numérico de uma função do primeiro grau;
- Comportamento de uma função do primeiro grau.
Para iniciar seus estudos sobre o conceito de função polinomial do primeiro grau, deve-se ter em mente que as funções são um conhecimento matemático que possui interdependência entre os seus valores desconhecidos, tratando-se de um conhecimento algébrico.
Para entender melhor sobre o assunto, acompanhe a situação a seguir:

No exemplo, percebe-se que a situação expressa o registro da idade e da altura de uma pessoa, sendo que, nos dados obtidos e registrados quanto maior era a idade de Júnior, maior era a sua altura. Nesta situação tem-se duas variáveis: a variável idade e a variável altura (dada em centímetros). Esse exemplo é conhecido como função, pois há uma relação de interdependência entre as variáveis.
Uma característica das funções é que elas podem ser representadas em uma tabela, como mostrou a imagem anterior, e, também na forma gráfica, como mostra a imagem a seguir, considerando as variáveis altura no eixo (y) e a idade em anos no eixo (x). Observe:
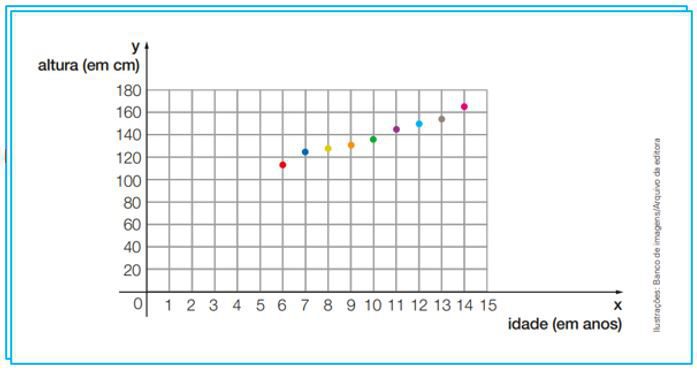
O gráfico nos permite tratar melhor as informações produzidas e registradas nas variáveis de altura e idade de Júnior, podendo localizar com precisão por meio dos pontos a idade e a altura correspondente de Júnior. Os gráficos utilizados nas funções que às expressam, possibilitam dar precisão e qualidade de demonstração dos dados obtidos.
Sobre a utilização dos gráficos com funções, faremos o uso do plano cartesiano, já amplamente trabalhado nos anos escolares anteriores.
No entanto, a imagem a seguir nos dá indícios e condições de uma revisão sobre as abscisas e ordenadas, mostrando como se localiza um ponto no plano cartesiano.
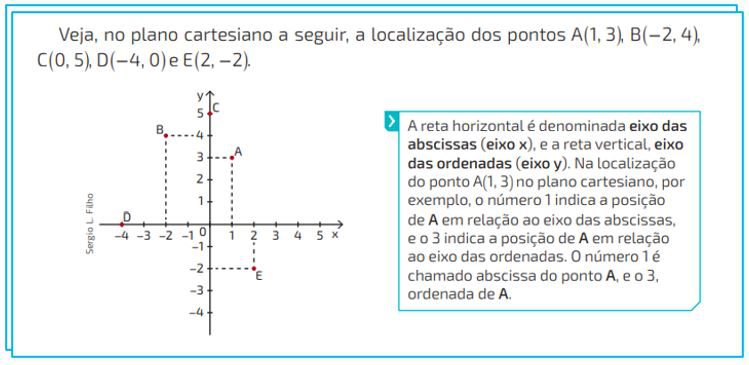
Assim, quando formos plotar uma função no plano cartesiano, devemos seguir essas coordenadas cartesianas, respeitando a ordem de posição primeiro no eixo x (abscissas) e depois eixo y (ordenadas).
Especificamente, as funções polinomiais do primeiro grau representam sempre uma reta no gráfico, conforme vamos analisar e estudar por meio do próximo exemplo. Acompanhe atentamente.
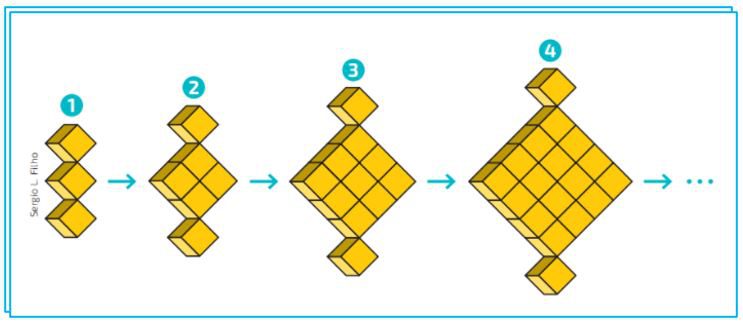
Na imagem anterior, tem-se uma sequência de figuras, que à cada figura nova da sequência aumenta-se a quantidade de cubinhos.
Para facilitar a compreensão desta sequência geométrica, vamos evidenciá-la de modo algébrico por meio de uma tabela, procurando desvelar a fórmula matemática que dê conta de expressar esse movimento em padrão dessa sequência:
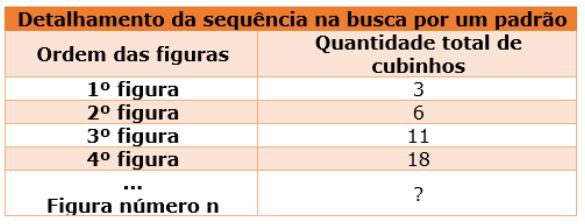
É interessante observar o formato geométrico e a quantidade de cubinhos que cada nova figura, na sequência, vai adquirindo. No formato geométrico é possível observar na figura 1 um quadrado de cubinho (1×1) no meio mais dois cubinhos nas extremidades verticais, na figura 2 um quadrado de cubinhos (2×2) mais dois cubinhos nas extremidades verticais, e assim sucessivamente aumentando a cada nova figura.
Com essa observação, pode-se pensar em uma outra tabela:
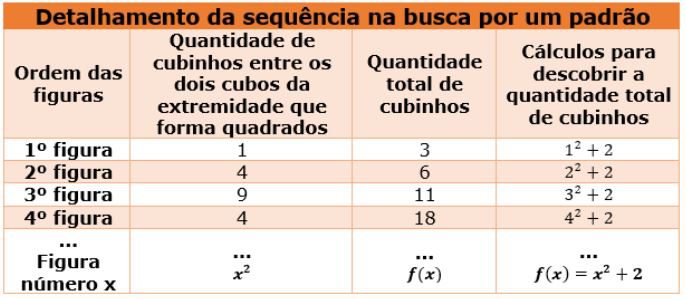
As funções são representadas pelo símbolo f(x), que quer dizer a função do valor de x, e, no caso da sequência geométrica acima, f(x) representa a quantidade total de cubinhos e x o número de ordem das figuras. Perceba que a há uma relação de interdependência entre as variáveis: quantidade total de cubinhos e número de ordem da figura, caracterizando como uma função polinomial, por tem-se em sua lei de formação um polinômio (x2+2), e, caracteriza-se por uma função polinomial do segundo grau, pois o expoente da parte literal é 2.
Nas funções que destinamos aos estudos desta atividade, o foco será dado em funções polinomiais do primeiro grau, ou seja, que a parte literal da lei de formação da função, seja, obrigatoriamente 1. As funções polinomiais do primeiro grau também podem receber o nome de função afim.
Agora é com você!
Questão 01. Analise atentamente a sequência geométrica abaixo e faça o que se pede:
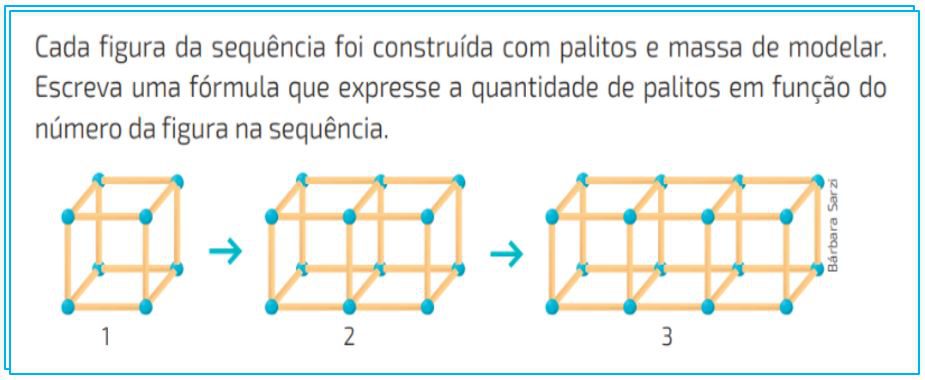
a) Preencha a tabela de forma correta, e informe ao final a lei de formação dessa função, representado por f(x) a quantidade total de palitos e por x, o número da sequência dessa figura:
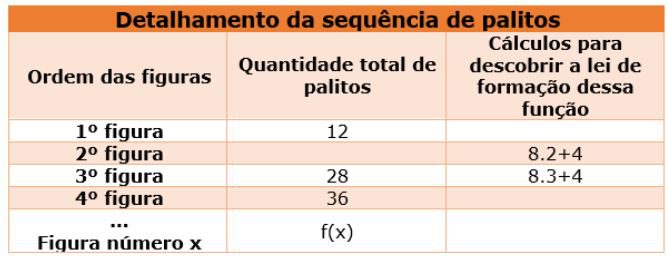
b) Agora observe a tabela e o plano cartesiano do comportamento dessa função graficamente para responder qual é o grau dessa função polinomial.
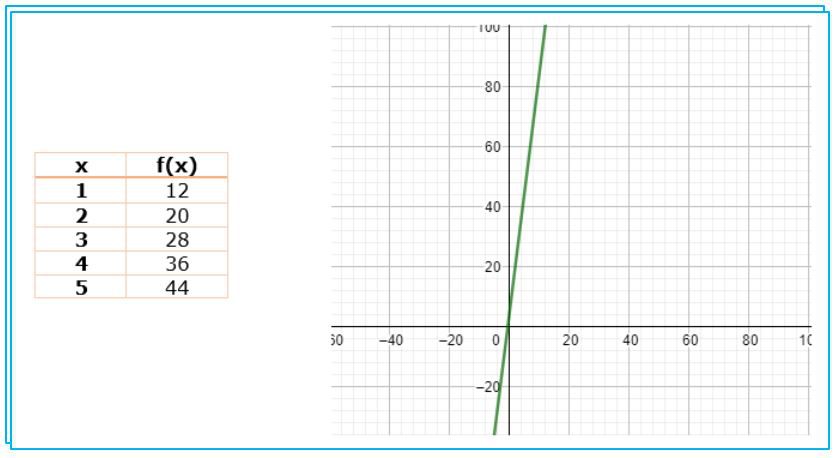
Uma outra característica das funções é que elas podem ser representadas por f(x), uma função de x, ou simplesmente por (y), conforme verifica-se na próxima situação:

Percebe-se com a situação da produção de queijos, que essa variável está intrinsecamente condicionada/interdependente com a quantidade, em litros, de leite, ressaltando a relação de lei de formação da função, onde y representa a quantidade de litros de leite utilizados na produção e x a quantidade de queijos que poderiam ser produzidos.
Observe a sua lei de formação, a tabela de organização de dados e a sua representação gráfica.
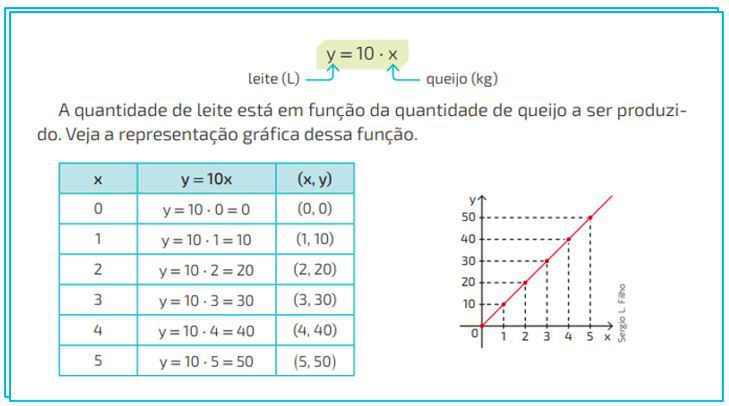
É importante destacar que, quanto mais queijo se produz, maior será o consumo de litros de leite, tratando-se, neste caso, de uma função crescente, pois o coeficiente da variável x é positivo e o gráfico aumenta-se para a direita.
Para saber se uma função polinomial do primeiro grau é crescente ou decrescente basta verificar a relação do sinal do coeficiente, como mostra o esquema:

Agora, observe graficamente o comportamento de uma função polinomial do primeiro grau, crescente ou decrescente.
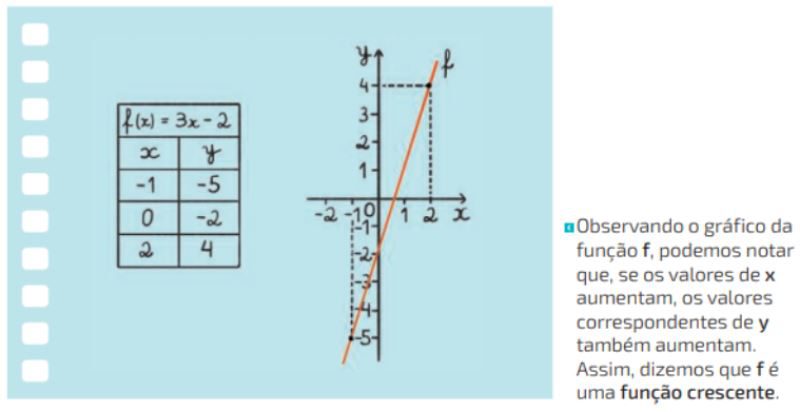
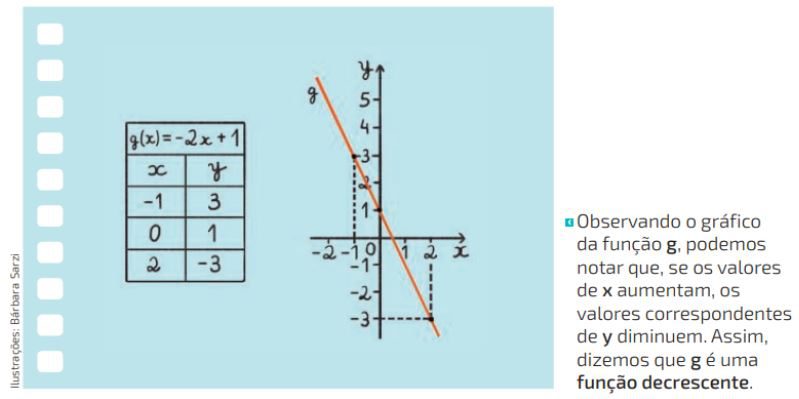
Viu como é fácil reconhecer se uma função polinomial do primeiro grau é crescente ou decrescente?
Agora é com você!
Coloque em prática os estudos de hoje realizando as questõesa seguir:
Questão 02. Em cada quadro estão representadas funções com valores de x e valores de y de uma função polinomial do primeiro grau. Analise atentamente as funções e descreva qual é a lei de formação de cada uma das funções:
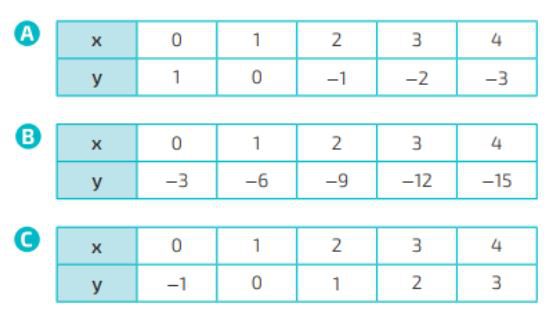
Questão 03. Tomando por base as funções do exercício anterior, mostre qual é o gráfico correspondente a cada uma das funções:
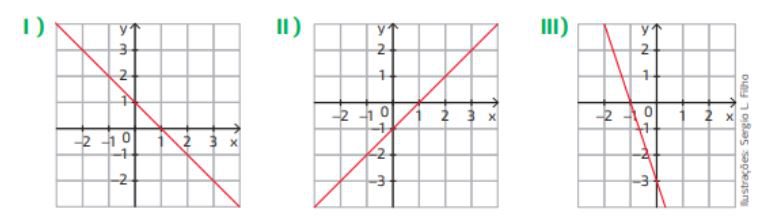
Questão 04. Ainda com base nas informações das duas últimas questões, identifique quais funções são crescentes. Justifique a sua resposta.
RELEMBRANDO!!!!!!!
Em síntese, nesta atividade de matemática você estudou sobre o conceito de função, compreendeu a função polinomial do primeiro grau, reconhecendo-a como função afim, identificou e diferenciou uma função polinomial do primeiro grau em crescente ou decrescente e aplicou os conceitos de funções a padrões geométricos de sequências recursivas.
Parabéns, continue com empenho em seus estudos matemáticos. Até a próxima atividade!
| Referências | IEZZI, Gelson., MACHADO, Antônio., DOLCE, Osvaldo. Matemática e realidade 9º ano – 9. ed. – São Paulo : Atual Editora, 2018. PATARO, Patricia Moreno., BALESTRI, Rodrigo. Matemática essencial 9o ano : ensino fundamental, anos finais – 1. ed. – São Paulo : Scipione, 2018. PNLD |
| Ciclo da adolescência Habilidades | Habilidades Estruturantes (EF09MA06-A) Descrever em contextos práticos as relações de proporcionalidade direta entre duas grandezas por meio de funções de 1° grau. (EF09MA06-B) Ler, interpretar, resolver e elaborar problemas com parte fixa e parte variável que podem ser expressas por funções do 1° grau, calculando valores numéricos e estabelecendo o comportamento da função (crescente ou decrescente) para um determinado intervalo de valores numéricos. Habilidade Complementar EF09MA06-H |