Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6º Ano do Ensino Fundamental – Anos Finais.
Equações de 1º grau com duas incógnitas
A equação linear com duas incógnitas, é uma expressão matemática de 1º grau que envolve dois valores desconhecidos. Estes valores desconhecidos são representados por letras chamadas de incógnitas ou variáveis. A equação demonstra a relação de dependência entre as incógnitas.
Veja este exemplo.
Camila comprou 2 sanduíches e 3 latas de refrigerante. O gasto total com este lanche foi R$60,00. Quais são os possíveis valores para o sanduíche e para o refrigerante?
Os preços do sanduíche e do refrigerante são desconhecidos, por isso, serão representados por letras (incógnitas):
- preço do sanduíche (x);
- preço do refrigerante (y).
A equação linear que representa o gasto total de Camila com o lanche, é
2x + 3y = 60.
Veja que os preços do sanduíche e do refrigerante podem variar, mas o valor total continuará o mesmo. Assim, fica claro que o preço do sanduíche (x) depende do preço do refrigerante (y).
Por exemplo, se o sanduíche custar R$15,00, qual será o preço do refrigerante?
2.15 + 3.y = 60
3y = 60 – 30
y = 30/3 => y = 10.
O refrigerante custará R$10,00. Neste caso, o par ordenado (15, 10) é solução para a equação. E esta, não é a única solução para a equação.
Solução da equação linear e a representação gráfica
Uma equação linear com duas incógnitas tem várias soluções. Cada solução é um par ordenado que, quando substituído na equação, torna a igualdade verdadeira.
Ainda pensando na situação problema descrita acima, vejamos outros pares de números que são solução para a equação 2.x + 3.y = 60.
Será que o par ordenado (12, 12) é uma solução para esta equação?
Para saber, é preciso substituir os valores na equação: x = 12 e y = 12.
2.x + 3.y = 60
2.12 + 3.12 = 60
24 + 36 = 60
Sim, o par ordenado (12, 12) é uma solução para a equação.
Na tabela, veja algumas soluções para esta equação linear.
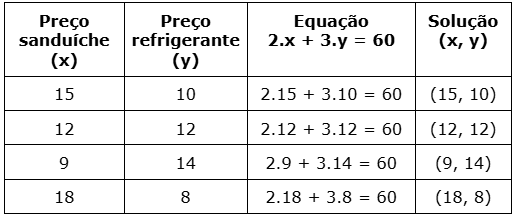
Usando o plano cartesiano para marcar os pares ordenados que são solução da equação, percebe-se que estes formam uma linha reta.
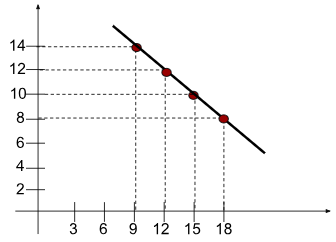
Todos os pontos sobre essa reta, são solução da equação linear.
Genericamente, a equação linear com duas incógnitas é representada por
a.x + b.y = c,
onde x e y são incógnitas e a, b, c são números chamados coeficientes.
Para reforçar os conceitos apresentados aqui, assista à videoaula “Equações lineares”, da professora Cristiane Souza, publicada a seguir.
Agora, utilize o que você aprendeu sobre esse assunto resolvendo as atividades a seguir.
QUESTÃO 1
Dentre as alternativas abaixo, é solução da equação linear x + 3.y = 20, o par ordenado
(A) (2, 6).
(B) (6, 2).
(C) (6, -2).
(D) (-2, 6).
QUESTÃO 2
Na padaria, comprei 1 café e 3 pães de queijo para o café da manhã. O total da minha conta foi de R$ 12,50.
- Se o preço de um café for representado por x.
- Se o preço de cada pão de queijo for representado por y.
a equação linear que representa o meu gasto total, é
(A) x + y = 12,50.
(B) x – y = 12,50.
(C) x – 3y = 12,50.
(D) x + 3y = 12,50.
QUESTÃO 3
Leia o cartaz com atenção.

Usando
- x para representar o preço da calça jeans e
- y para representar o preço de cada camiseta,
faça:
A) Escreva a equação que representa o total da compra da promoção.
B) Se o preço da calça jeans na promoção for R$70,00, qual é o preço de cada camiseta?
QUESTÃO 4
Dada a equação 5x + 3y = 30,
A) complete a tabela com dois pares ordenados (x, y) que sejam solução para a equação.

B) represente no plano cartesiano, os pares ordenados da tabela anterior. Lembre-se de ligar os pontos.
Obs.: Com uma régua, desenhe o plano cartesiano e ligue os pontos representados.
QUESTÃO 5
Uma plataforma de anúncios de vendas on-line cobra R$3,00 por dia mais R$2,00 por imagem publicada.
Clóvis anunciou sua moto nesta plataforma e o gasto total foi de R$90,00 pelo anúncio.
Considere x para o número de dias que o anúncio ficou no ar e y para a quantidade de fotos publicadas.
A) Escreva a equação linear que representa o preço total pago por Clóvis pelo anúncio da moto nesta plataforma.
B) Se o anúncio da moto ficou no ar por 20 dias, quantas fotos Clóvis publicou?
| Autoria | Cristiane Soares de Souza |
| Formação | Matemática – Licenciatura |
| Componente curricular | Matemática |
| Habilidade(s) | (EF08MA07) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano. |
| Descritor(es) | D33 – Identificar uma equação ou inequação do 1° grau que expressa um problema. |
| Objeto(s) de conhecimento | Equação linear de 1º grau com duas incógnitas; valor numérico da equação linear de 1º grau; representação geométrica/gráfica de equação linear de 1° grau, com duas incógnitas (plano cartesiano). |
| Referência(s) | ROSA, Andrea Stephanie Moreira. et al. Brincando com a álgebra: o uso de jogos no ensino de sistemas de equações lineares. TANGRAN Revista de Educação Matemática. Dourados, MS, vol 3, nr 4, pp 173 – 188 (2020). Acessado na URL https://ojs.ufgd.edu.br/tangram/article/view/10968/6515 em 03/06/2025. RODRIGUES, Rodrigo Júnior. Aprendizagem significativa de sistemas de equações de 1º grau: uma sequência didática para alunos do ensino fundamental. 2021. Universidade Federal de Uberlândia. Acessado na URL https://repositorio.ufu.br/bitstream/123456789/33514/3/AprendizagemSignificativaSistemas.pdf em 03/06/2025. |

