Olá, estudante! Esta videoaula de Matemática para o 8º ano do Ensino Fundamental foi veiculada na TV no dia 26/05/2021 (Quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Olá estudante do 8º ano, nesta atividade você irá estudar sobre as equações polinomiais do primeiro grau, aprofundando os conhecimentos em equações com duas variáveis e representá-las como um sistema de equações, mostrando a relação de dependência entre uma e outra, além de fazer resoluções gráficas desse tipo de sistema de equação.
Venha iniciar seus estudos, você não pode ficar fora dessa!
Assista a videoaula a seguir com a temática: Equações e Sistema de Equações polinomiais do primeiro grau
Olá, nesta atividade de matemática você vai estudar sobre as equações e sistema de equações polinomiais do primeiro grau, ressaltando:
- Formas de resolver uma equação polinomial do primeiro grau;
- Situações problemas envolvendo equações;
- Sistema de equações com duas variáveis;
- Métodos de resolução de um sistema de equações;
- Resolução gráfica de um sistema de equações.
Para iniciar seus estudos é importante lembrar que a equação faz parte de um estudo maior que refere-se à álgebra, acompanhe a explicação sobre o que é uma equação:
Equação é uma sentença matemática expressa por uma igualdade em que há pelo menos uma letra que representa um valor desconhecido, chamada incógnita. Resolver uma equação é determinar o valor desconhecido da incógnita, ou seja, obter a solução ou a raiz da equação.
Para exemplificar o contexto de uma equação observe o exemplo a seguir:
Exemplo1:
Rafael possui R $43,50, sendo R$17,50 em moedas e o restante em cédulas de 2 reais.

Podemos determinar, por meio de uma equação, quantas cédulas de 2 reais Rafael possui. Para isso, indicamos por x a quantidade de cédulas de 2 reais e escrevemos a equação:
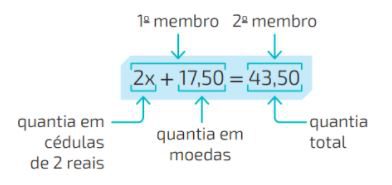
Podemos resolver essa equação utilizando os princípios aditivo e multiplicativo da igualdade.
Lembre-se de que pelo princípio aditivo a igualdade se mantém ao adicionarmos ou ao subtrairmos um mesmo número dos dois membros de uma equação. E pelo princípio multiplicativo, a igualdade se mantém ao multiplicarmos ou dividirmos os dois membros da equação pelo mesmo número diferente de zero.

Portanto, Rafael possui 13 cédulas de 2 reais.
Agora é a sua vez!
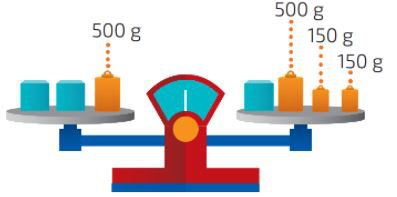
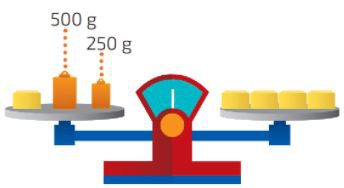
Questão 01. A balança a seguir está em equilíbrio. Nela, as caixas azuis possuem massas com a mesma medida. Sabendo que nessas balanças, caixas de mesma cor possuem medidas de massa iguais, elabore uma equação e resolva-a em cada um dos casos:

Questão 02. Natália pagou R $315,00 pelas três peças de roupa a seguir.

Sabendo que as calças têm preços iguais e que a saia custou metade do preço da calça:
a) escreva uma equação que represente essa situação.
b) determine o preço pago por Natália em cada peça de roupa.
Agora que você já sabe o que é uma equação do primeiro grau, inclusive consegue resolvê-la, vamos ampliar nossos estudos para equações do primeiro grau com duas variáveis.
Para começar esse estudo, acompanhe a situação a seguir:

Podemos resolver esse problema utilizando uma equação. Para isso, indicamos por x e por y os números procurados.
x + y = 6
A seguir, temos alguns possíveis valores de x e de y.
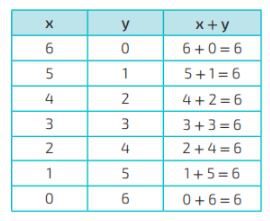
As soluções de uma equação do 1o grau com duas incógnitas são pares ordenados. Em relação à equação x + y = 6 , os pares ordenados (6, 0) , (5, 1) , (4, 2) , (3, 3) , (2, 4) , (1, 5) e (0,6) são algumas de suas soluções.

Note que se ligarmos cada um dos pontos obtidos com as coordenadas que eram solução da equação, tem-se uma reta:
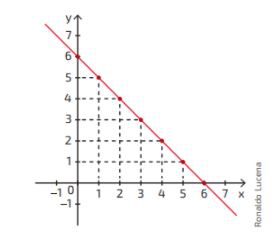
Agora é com você!
Questão 03. Observe a reta formada no plano cartesiano:
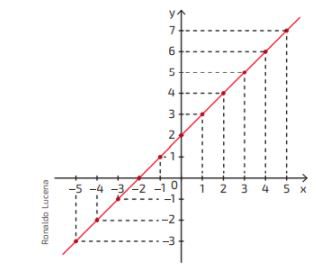
Essa reta representa as soluções de qual das equações?
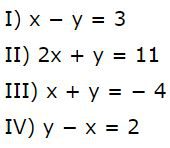
Agora vamos ver quando se duas equações com duas variáveis cada uma, estudando o conceito matemático de sistemas de equações.
Para aprofundar os estudos nos sistemas de equações observe com atenção a situação a seguir:
Em um estacionamento, entre carros e motos, há 12 veículos, sendo a maioria carros. A diferença entre a quantidade de carros e o dobro da quantidade de motos é igual a 3.
Quantos carros e quantas motos há nesse estacionamento?
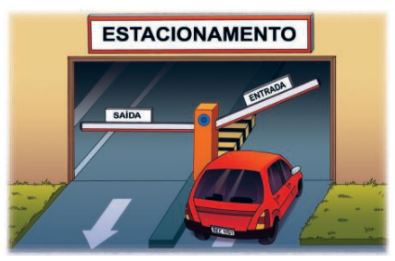
Podemos resolver essa questão escrevendo duas equações: uma para representar a quantidade total de veículos no estacionamento e outra para representar a diferença entre a quantidade de carros e o dobro da quantidade de motos.
Para isso, chamamos de x a quantidade de carros e de y a quantidade de motos.

Indicamos o sistema de equações da seguinte forma:
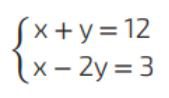
Para resolver esse sistema, pode-se utilizar o método da substituição:


Perceba, que, se atribuirmos valores para cada uma das equações, iremos ter vários pares ordenados, e se colocarmos no gráfico os pontos obtidos em cada uma das equações, as retas correspondentes a cada uma delas vão ser concorrentes, ou seja, vão se cruzar em um único ponto, este, ponto é o ponto exato da resolução do sistema de equações, já que é o ponto comum da resolução de uma e outra equação ao mesmo tempo, satisfazendo as duas equações.
Agora chegou a sua vez de colocar todos os estudos desta atividade em prática, resolvendo as questões:
Questão 04. Leia o problema e, em seguida, responda às perguntas:

Questão 05. Adriana e Felipe possuem juntos a quantidade de CDs indicada na figura, sendo que Adriana possui 4 CDs a mais que Felipe. Chamando de x a quantidade de CDs de Adriana e de y a quantidade de CDs de Felipe, escreva um sistema de duas equações do 1o grau com duas incógnitas que possibilite determinar a quantidade de CDs de cada um deles.

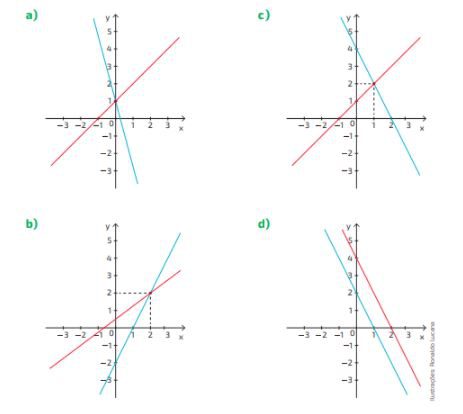
Questão 06. Qual dos gráficos mostra a solução do sistema:
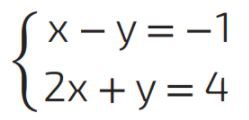
Parabéns pelo empenho em resolver as questões propostas!
RELEMBRANDO!!!!!!!
Nesta atividade de matemática, você estudou sobre os conhecimentos algébricos, sobretudo, sobre os conhecimentos de equações do primeiro grau com uma e duas incógnitas. Percebeu que as equações do primeiro grau com duas incógnitas podem ter infinitas respostas, por isso, o valor desconhecido delas é chamado de variável. Já um sistema de equações do primeiro grau pode ter apenas uma única solução que satisfaça as duas equações, por isso o seu valor desconhecido é chamado de variável. Há casos específicos que sistemas de equações não geram um resultado, ou, há casos que todas as soluções de uma são também solução da outra equação, nas próximas aulas exploraremos esses casos.
Parabéns pelo estudo, continue se empenhando com as atividades do conexão escola. Até a próxima atividade de matemática!
| Habilidades | Habilidade Estruturante (EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso. Habilidades complementares EF08MA06- E EF08MA07 GO-EF08MA28 EF08MA09 |
| Referências: | DANTE, Luiz Roberto. Teláris matemática, 8º ano: ensino fundamental, anos finais – 3. ed. – São Paulo : Ática, 2018. PATARO, Patricia Moreno., BALESTRI, Rodrigo. Matemática essencial 8o ano : ensino fundamental, anos finais – 1. ed. – São Paulo : Scipione, 2018. PLND |
Professor, essa aula segue a Matriz Curricular das Habilidades Estruturantes 2021-2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido à pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 147/2020 Dirped).

