Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento I (9º ano) do Ciclo da adolescência foi veiculada na TV no dia 27/05/2021 (Quinta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 9º ano, irá estudar sobre as equações polinomiais do segundo grau, compreendendo algumas situações problemas que envolvem esse tipo de equação, inclusive, realizando algumas demonstrações algébricas para se chegar a resolução de Bhaskara e resolução geométrica.
Você não pode ficar fora dessa!
Assista a videoaula a seguir com a temática: ÁLGEBRA E FUNÇÕES
Olá estudante do nono ano da Rede Municipal de Educação da Cidade de Goiânia. Nesta atividade de matemática você vai estudar sobre as equações polinomiais do segundo grau, ressaltando:
- O que é uma equação do segundo grau;
- Equações do segundo grau: completas e incompletas;
- Resolução de situações problemas envolvendo equações do segundo grau;
- Resolução algébrica da equação do segundo grau pelo método babilônico de completar quadrados e método de Bhaskara;
Para iniciar seus estudos sobre as equações do segundo grau, analise a situação abaixo:
Certo satélite artificial fotografou uma região da Terra de formato quadrado, medindo 625 m 2 de área. Qual é a medida do comprimento do lado da região fotografada pelo satélite?
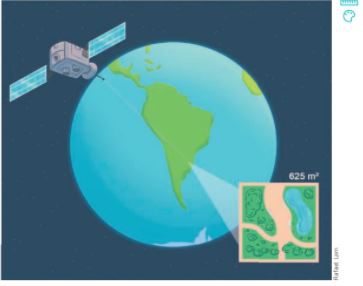
Para resolver o problema, representamos por x a medida do comprimento do lado da região fotografada e escrevemos a equação:
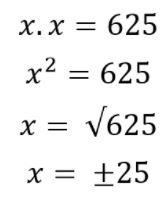
Nesse caso, x corresponde à medida do lado da região, que deve ser positiva. Assim, desconsideramos o valor negativo − 25 .
Portanto, a região fotografada tem 25 m de medida de comprimento de lado. Na equação, o maior expoente da incógnita é 2.
Dizemos que essa é uma equação do 2o grau com uma incógnita.
Uma equação do segundo grau completa possui três termos, conforme mostra a imagem abaixo:
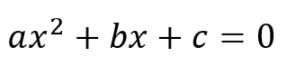
No entanto, as equações do segundo grau, também podem aparecer em sua forma incompleta, conforme mostra o quadro abaixo:

Questão 01. Sobre as equações do segundo grau, e, conforme estudado até o momento, quais das equações abaixo são do segundo grau?
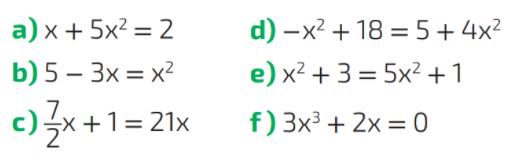
Questão 02. Escreva uma equação do 2º grau na forma reduzida que representa a medida da área de um quadrado cujo comprimento do lado mede 2x + 1 cm é igual a 16 centímetros quadrados.
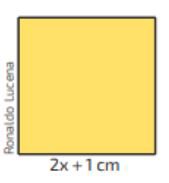
Para resolver esse problema, basta multiplicar o lado do quadrado por ele mesmo, colocando essa multiplicação igual ao valor da área do quadrado:
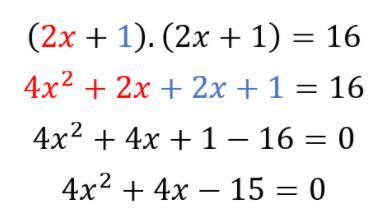
Resolvendo uma equação do segundo grau incompleta em b
Uma equação do segundo grau, incompleta em b, tem a forma geral:
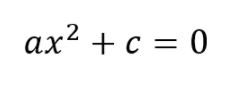
Agora, observe como procedemos para sua resolução:

Assim, as raízes (solução) da equação é {-8 e +8}
Resolvendo uma equação do segundo grau incompleta em c
Uma equação do segundo grau incompleta em c, tem a forma geral:
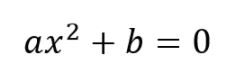
Agora observe o seu processo de resolução:

Assim, as raízes (solução) da equação é {0 e 8}
Agora que você já sabe como resolver equações incompletas em b ou c, resolva a questão abaixo:
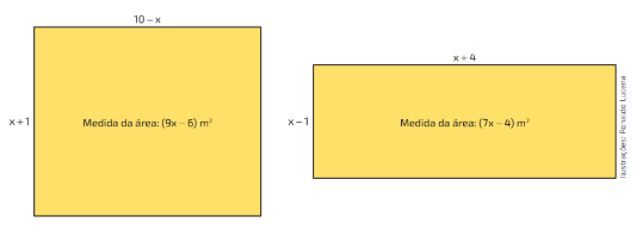
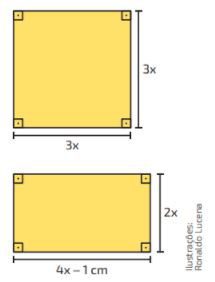
Questão 03. Determine a medida do comprimento dos lados de cada retângulo.
Resolvendo equações completas
Para resolver equações completas na forma:
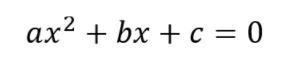
Existem vários métodos, nesta atividade você aprenderá dois métodos de resolução: o método de completar quadrados, também conhecido como método babilônico de resolver equações do segundo grau e método de Bhaskara.
Resolvendo uma equação do segundo grau completa: método de completar quadrados
Há equações do 2o grau em que o 1o membro não é um trinômio quadrado perfeito. Nesses casos, podemos determinar as raízes da equação utilizando o método de completar quadrados.
Tomamos como exemplo a equação:

Logo, a solução da equação é {-7 e -1}
Resolvendo uma equação do segundo grau completa: método de Bhaskara
Outra maneira de resolver uma equação do 2º grau é por meio da fórmula resolutiva, que consiste na generalização do método de completar quadrados.
Utilizando essa fórmula, é possível obter as raízes de uma equação do 2º grau por meio de seus coeficientes.
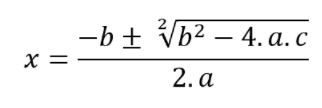

Agora é com você, resolva as questões abaixo envolvendo equações do segundo grau completas:
Questão 04. Determine as raízes de cada equação pelo método de completar quadrados.
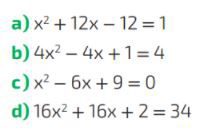
Fonte: (PATARO & BALESTRI, 2018, p. 47) PNLD
Questão 05. Sabendo que a medida da área do quadrado é 8 centímetros quadrados maior do que a medida da área do retângulo, calcule o valor de x.
RELEMBRANDO!!!!!!!
Em síntese, nesta atividade de matemática você estudou alguns conhecimentos algébricos, ressaltando as equações polinomiais do segundo grau, estudando e identificando uma equação do segundo grau completa ou incompleta, desenvolvendo cálculos necessários para a sua resolução.
Parabéns, continue com empenho em seus estudos matemáticos. Até a próxima atividade!
| Habilidades | Habilidade Estruturante (EF09MA06-E) Aplicar a fórmula de Bhaskara para resolver equações do 2° grau associadas às funções quadráticas Habilidades Complementares EF09MA06 C EF09MA06 D EF09MA06 F EF09MA06-G |
| Referências: | IEZZI, Gelson., MACHADO, Antônio., DOLCE, Osvaldo. Matemática e realidade 9º ano – 9. ed. – São Paulo : Atual Editora, 2018. PATARO, Patrícia Moreno., BALESTRI, Rodrigo. Matemática essencial 9o ano : ensino fundamental, anos finais – 1. ed. – São Paulo : Scipione, 2018. PNLD |
Professor, essa aula segue a Matriz Curricular das Habilidades Estruturantes 2021-2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido à pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 147/2020 Dirped).

