Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAGIBTzqMLo/tzQW5myS5rQu3srjgFvA3w/edit?utm_content=DAGIBTzqMLo&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
Imagine em um parque de diversões uma enorme roda-gigante girando lentamente. Ou em um jogo de basquete a bola descrevendo um arco perfeito antes de entrar na cesta. Em ambos os casos, temos aplicações práticas de um dos conceitos mais importantes da geometria: a circunferência.
Elementos Básicos de uma Circunferência
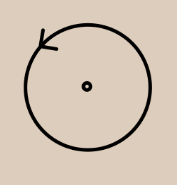
Uma circunferência é uma linha curva fechada em que todos os pontos estão à mesma distância de um ponto fixo chamado centro. A seguir vejamos seus elementos:
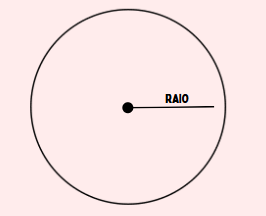
Raio
O raio é a distância do centro da circunferência até qualquer ponto da linha. Se você imaginar uma bicicleta, o raio seria a distância do centro da roda até o pneu.
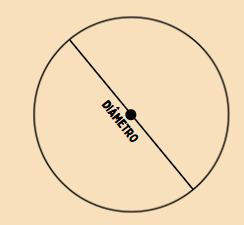
Diâmetro
O diâmetro é uma linha reta que passa pelo centro da circunferência e toca dois pontos opostos na linha da circunferência. O diâmetro é o dobro do raio. Pense em cortar uma pizza exatamente no meio; a linha de corte representa o diâmetro.
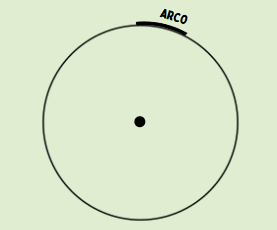
Arco
O arco é uma parte da circunferência entre dois pontos contidos nela.
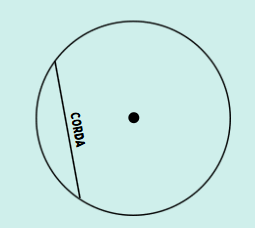
Corda
A corda é uma linha reta que conecta dois pontos da circunferência. Se você pegar um pedaço de fita e colá-lo em dois pontos da borda de uma tampa redonda, a fita representa uma corda.
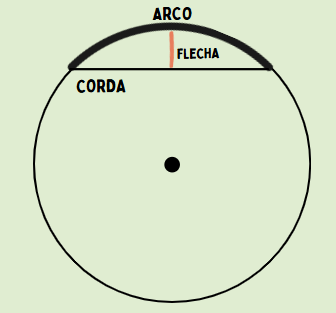
Flecha
A flecha é a distância máxima entre o arco e a corda que o subtende.
Aplicações Práticas
Na engenharia, por exemplo, ao projetar rodas, engrenagens e arcos é necessário conhecimento sobre circunferência. Na arquitetura, ao desenhar cúpulas e arcos de pontes. E até na arte, onde artistas desenham círculos perfeitos para criar obras de arte impressionantes.
Exercícios Resolvidos
Vamos resolver alguns exercícios para consolidar esses conceitos.
Exemplo 1: Ana está andando de bicicleta no parque. A roda da bicicleta dela tem um diâmetro de 70 cm. Qual é o raio da roda?
Resolução – Como o raio é metade do diâmetro, faremos:
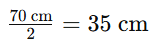
Resposta – O raio da roda de Ana mede 35 cm.
Exemplo 2: Em um parque de diversões a roda-gigante tem um raio de 25 metros. Qual é o diâmetro da roda-gigante?
Resolução – Como o diâmetro é o dobro do raio, temos que:
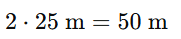
Resposta – O diâmetro da roda-gigante é de 50 metros.
Agora que você , que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Em um parquinho infantil, há um círculo de areia com um diâmetro de 12 metros. O raio do círculo de areia é
(A) 3 metros.
(B) 6 metros.
(C) 12 metros.
(D) 24 metros.
QUESTÃO 2
O mostrador de um relógio de parede tem uma corda que mede 20 cm, e essa corda divide o relógio ao meio. O diâmetro do relógio é
(A) 10 cm.
(B) 20 cm.
(C) 30 cm.
(D) 40 cm.
QUESTÃO 3
Em um jardim circular, há um caminho que liga dois pontos na borda do jardim. Como esse caminho é chamado? Faça um desenho representando essa situação.
QUESTÃO 4
Um relógio de parede tem ponteiros que se movem ao longo de sua circunferência. Qual é o nome da linha imaginária que conecta o centro do relógio até qualquer ponto na circunferência?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA22-B) Identificar os elementos básicos de uma circunferência, tais como raio, diâmetro, arco, flecha e corda, e suas diversas aplicações em resoluções de problemas. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |
