Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Disponível em: <Contador Contabilidade Conselheiro – Foto gratuita no Pixabay – Pixabay>- último acesso em 22 de maio de 2023.
Dízima periódica simples
Os números racionais são aqueles que podem ser representados na forma fracionária, onde o numerador é um número inteiro e o denominador é um número inteiro diferente de zero.
Quando representados na forma decimal, eles podem ser um número com casas decimais finitas. A fração ¾, por exemplo, ao efetuarmos a divisão de 3 por 4, obtemos o número decimal 0,75, que tem duas casas decimais, ou seja, dois algarismos após a vírgula.
Caso o número decimal tenha casas decimais infinitas e periódicas, ele é uma dízima periódica. É o caso do número 0,33333… que resulta da divisão do numerador pelo denominador da fração 1/3.
Uma dízima periódica é considerada simples quando na parte decimal temos apenas o(s) algarismo(s) que se repete(m) infinitamente. Como os números 0,77777…. e 1,525252…
Exemplos:
0, 222222…
1,55555….
2,454545…
Fração geratriz de uma dízima periódica:
Podemos determinar a representação fracionária de uma dízima periódica, a que chamamos de fração geratriz da dízima periódica.
O numerador é obtido subtraindo-se a parte não periódica da parte periódica da dízima periódica simples, enquanto o denominador é representado por uma sequência de “noves” equivalente ao número de algarismos na parte periódica. Veja como determinar a fração geratriz da dízima 0,555555….:
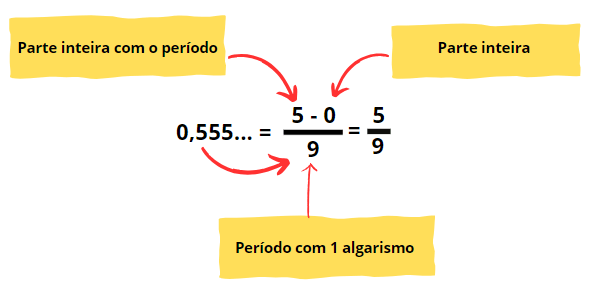
Outros exemplos:
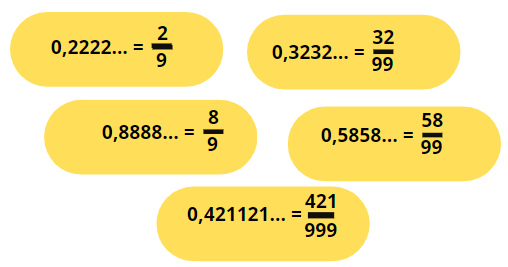
Agora que você estudou sobre as dízimas periódicas simples, que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Juliana economizou dinheiro por 6 meses e conseguiu uma quantia de 1000 reais. Responda:
a) Se ela tivesse juntado quantia igual mensalmente, qual seria o valor referente a cada mês?
b) Esse número obtido é um número racional? Por que?
QUESTÃO 2
Para fazer uma receita de bolo, Mauro precisava usar 1/3 de uma xícara de açúcar e 1/3 de uma xícara de farinha de trigo. Ele ficou curioso para saber que número decimal corresponde a soma das quantidades desses ingredientes. Ao adicionar os números 1/3 +1/3 e escrever o resultado na forma decimal ele obteve:
(A) 0,3333…
(B) 0,6666…
(C) 0,4444…
(D) 0,9999…
QUESTÃO 3
Em uma competição de natação observou-se que um atleta completava cada volta em 0,5555… segundos. Mantendo esse mesmo padrão, quantos segundos ele levaria para completar 8 voltas?
(A) 4,444… s
(B) 4,555… s
(C) 4,666… s
(D) 4,777… s
QUESTÃO 4
Um cientista mediu a quantidade de água que evapora de um recipiente a cada segundo e obteve o valor de 0,8888… mL. Qual a representação fracionária dessa quantidade?
| Autoria: | Priscilla Nascimento Dias, licenciada em Matemática e Pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA02-B) Aplicar a localização de números racionais para estimar a localização de alguns números irracionais na reta numérica. (EF09MA02-C) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica em situações diversas. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; 1° Bimestre; Goiânia, 2023. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2023. |