Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.
Disponível em: <Volta Às Aulas Educação Aprendendo – Imagens grátis no Pixabay> acesso em 03 de março de 2022.
O estudo dos números é fundamental para compreendermos as relações matemáticas que permeiam diversas áreas do conhecimento. Nesse contexto, destacam-se conjuntos importantes: os números naturais, inteiros, racionais, irracionais e reais. Vejamos um pouco sobre alguns deles:
Conjunto dos Números Reais:
O conjunto dos números reais, denotado por ℝ, abrange todos os números que podem ser representados na reta numérica. Isso inclui os números racionais e irracionais, tornando-o um conjunto abrangente e contínuo. Cada ponto na reta numérica corresponde a um número real, seja ele positivo, negativo ou zero.
Conjunto dos Números Racionais:
Os números racionais são aqueles que podem ser expressos como uma fração, onde o numerador e o denominador são inteiros e o denominador não é zero. Por exemplo, 3/4, -2, e 5 são números racionais. O conjunto dos números racionais é denotado por ℚ. Frações simples, como 1/2 ou 3/5, pertencem a esse conjunto, mas também estão inclusas frações geratrizes.
Fração Geratriz:
Uma fração geratriz é uma forma especial de representar um número racional. Ela é obtida por meio de um processo chamado expansão decimal periódica. Por exemplo, a fração geratriz do número 1/3 é 0.333…, indicando que o algarismo 3 se repete indefinidamente. Outro exemplo é a fração geratriz de 5/7, que resulta em 0.714285…, onde os algarismos 714285 se repetem ciclicamente. Esse método permite representar de maneira concisa e precisa certos números racionais.
Números Irracionais:
Os números irracionais têm expansões decimais não periódicas e infinitas, tornando impossível representá-los como uma razão de dois inteiros. Exemplos clássicos de números irracionais incluem a raiz quadrada de 2 (√2), π (pi) e e (número de Euler). A irracionalidade desses números implica que suas representações decimais não se repetem ou terminam, fornecendo uma riqueza infinita de informações na reta numérica.
Assista a videoaula da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
Sabemos que as dízimas periódicas simples ou compostas são números racionais, pois podem ser representadas na forma fracionária. Então, o resultado da adição 0,4444… + 0,2222… é:
(A) 5/9
(B) 2/3
(C) 3/5
(D) 4/9
Questão 2
Ana dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 2,3333… Isso significa que ele efetuou qual das divisões a seguir?
(A) 7:3
(B) 2:3
(C) 4:3
(D) 5:3
Questão 3
Escreva um elemento que represente cada um dos conjuntos numéricos representados na figura:
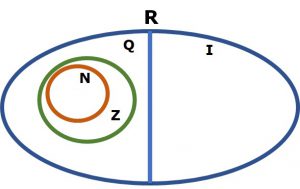
Imagem do arquivo pessoal
Questão 4
O resultado da seguinte subtração das dízimas periódicas 1, 666… – 0,888… é:
(A) 7/9
(B) 3/5
(C) 5/9
(D) 4/9
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA01) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade). (EF09MA01-A) Compreender que existem problemas, especialmente alguns vinculados à geometria e medidas, cujas soluções não são dadas por números racionais (caso do π, da √2, √3 etc.). (EF09MA02-A) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica, dízima periódica, e que pode ser escrita em forma de fração irredutível a/b, com b diferente de zero. (EF09MA02-B) Aplicar a localização de números racionais para estimar a localização de alguns números irracionais na reta numérica. (EF09MA02-C) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica em situações diversas. |
