Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 7º ano do Ensino Fundamental.

Disponível em: < Bolsa De Valores Economia Mundial – Imagens grátis no Pixabay > Acesso em: 01 de agosto de 2022.
Os números negativos surgiram da necessidade de representar quantidades que faltavam. Eles são menores do que zero e são usados em cálculos bancários, temperaturas muito frias, saldo de gols em campeonatos de futebol, entre outros.
Definição e Representação:
Os números inteiros constituem um conjunto fundamental na matemática, representando uma ampla gama de valores que incluem números positivos, negativos e o zero.
Sua representação na reta numérica evidencia a dualidade entre positivos à direita e negativos à esquerda, com o zero como ponto de transição. Matematicamente, o conjunto dos números inteiros é denotado por ℤ.
Uso no Dia a Dia:
A presença dos números inteiros é onipresente na vida cotidiana. Desde as temperaturas, marcadas em graus Celsius ou Fahrenheit, até as transações financeiras, onde valores positivos representam ganhos e negativos, perdas. Contar objetos, quantificar dívidas, calcular distâncias em coordenadas geográficas, são apenas alguns exemplos que ilustram a aplicabilidade direta dos números inteiros em diversas situações do dia a dia.
Adição e Subtração:
A soma de dois inteiros do mesmo sinal resulta em um número com o mesmo sinal, enquanto a soma de inteiros com sinais opostos exige a subtração dos valores absolutos, preservando o sinal do número de maior magnitude.
Exemplos:
(+5) + (−3) = +2
(−8) − (+2) = −10
(−6) + (−9) = −15
(+12) − (−7) = 12 + 7 = 19
Multiplicação:
A multiplicação de inteiros é regida por regras específicas. O produto de dois números com sinais iguais é positivo, enquanto a multiplicação de números com sinais diferentes resulta em um produto negativo.
Exemplos:
(−4) . (+6) = −24
(−4 ) . (−3) = 12
Divisão:
A divisão entre inteiros segue as mesmas regras de sinais da multiplicação.
Exemplos:
(−12) : (+6) = −2
(−20 ) : (−5) = 4
Assista a videoaula com a professora Priscilla com essa temática
Vamos responder algumas questões?
Questão 1
A imagem a seguir mostra um extrato bancário. Calcule o saldo final dessa conta no final de todas essas movimentações:
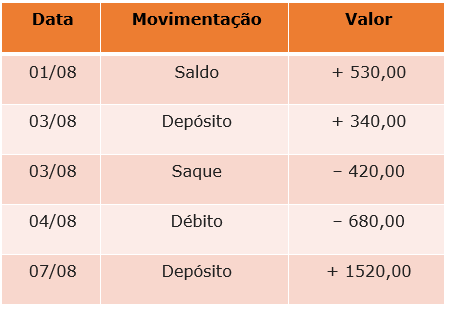
Imagem do arquivo pessoal
Questão 2
Leia o texto a seguir para responder as perguntas:
A cidade de “A” pode registrar temperaturas abaixo de zero grau em onda de frio. O povoado “B” será a região com as menores temperaturas, que começam a cair na quarta-feira (18) podendo chegar a -2 ºC e a cidade “A” a 4ºC.
Responda:
- Qual foi a menor temperatura indicada no texto?
- Essa temperatura foi abaixo de zero?
- Represente na reta numérica as duas temperaturas presentes no texto.
Questão 3
Você está gerenciando seu orçamento doméstico e se depara com as seguintes transações:
Pagamento da conta de luz: −50 reais
Recebimento de uma quantia extra de dinheiro: +30 reais
Compra de mantimentos: −25 reais
O saldo total após essas transações é
(A) −45 reais
(B) +55 reais
(C) −5 reais
(D) +5 reais
Questão 4
Durante uma semana de inverno, as temperaturas diárias são registradas da seguinte forma:
- Segunda-feira: −3 graus Celsius
- Terça-feira: +5 graus Celsius
- Quarta-feira: −2 graus Celsius
- Quinta-feira: +1 grau Celsius
A temperatura média nesses quatro dias é:
(A) −0,5 graus Celsius
(B) +0,5 graus Celsius
(C) −1,5 graus Celsius
(D) +1,5 graus Celsius
Questão 5
Paulo esqueceu de pagar uma dívida de R$ 240,00 no banco e descobriu que após 1 ano essa dívida triplicou. De acordo com essas informações responda:
- Qual a representação dessa situação por meio de uma multiplicação com números inteiros?
- Qual o resultado dessa multiplicação?
- Se ele resolver dividir em 4 parcelas iguais, qual será o valor de cada uma?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA03-A) Reconhecer significados dos números inteiros em diferentes contextos, como aqueles que indicam falta, diferença, orientação (origem) e deslocamento entre dois pontos. (EF07MA03-B) Reconhecer a distância de um número inteiro dado em relação à origem da reta numérica, módulo de um número inteiro, relacionando números opostos simétricos. (EF07MA03-C) Ler, escrever, comparar e ordenar números inteiros em diferentes contextos, incluindo o histórico, e associá-los a pontos da reta numérica. (EF07MA03-D) Utilizar as operações de adição e subtração de números inteiros e as suas respectivas propriedades, em situações diversas. (EF07MA03-E) Utilizar as operações de multiplicação e divisão de números inteiros e as suas respectivas propriedades, em situações diversas. (EF07MA03-F) Utilizar as operações de potenciação e radiciação de números inteiros e as suas respectivas propriedades, identificando-as como operações inversas, em situações diversas. (EF07MA04-A) Ler, interpretar e resolver problemas que envolvam operações com números inteiros. (EF07MA04-B) Elaborar problemas com números inteiros envolvendo os diferentes significados das operações e suas aplicações em situações diversas. Exemplo: interpretar uma situação climática através de uma dada temperatura, analisar altitudes e profundidades em relação ao nível do mar, avaliar os diversos tipos de saldo como saldo de gols em um campeonato, saldo bancário após uma série de operações, entre outros. |
