Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8º Ano do Ensino Fundamental – Anos Finais.
CONGRUÊNCIA DE TRIÂNGULOS
Você já observou como duas peças de um quebra-cabeça se encaixam perfeitamente? Isto tem relação com um conceito matemático: a congruência.
O conceito de congruência é usado como referência a elementos que têm medidas iguais. Por exemplo:
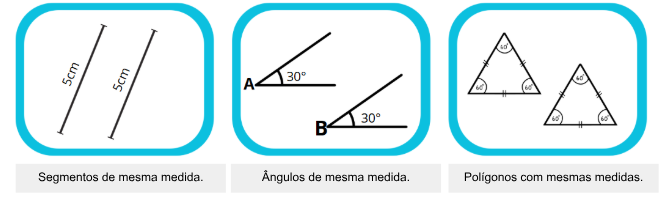
Se sobrepor esses elementos, eles vão se encaixar direitinho sem sobrar e nem faltar nada.
Congruência entre triângulos.
Dizemos que dois triângulos são congruentes quando eles têm exatamente o mesmo formato e o mesmo tamanho. Isso quer dizer que todas as suas medidas são iguais. Assim, os lados e os ângulos de um triângulo são iguais aos lados e aos ângulos do outro.
Como saber se dois triângulos são congruentes?
O triângulo é um polígono rígido, ou seja, uma vez definidos os tamanhos dos lados e dos ângulos, esse polígono não se modifica. Por isso, para saber se dois triângulos são congruentes, não é preciso comparar todos os lados e nem todos os ângulos. Podemos utilizar os chamados casos de congruência que ajudam nessa identificação com base em algumas informações. Por exemplo:
- Se os três lados forem iguais (caso Lado-Lado-Lado);
- Se dois lados e o ângulo entre eles forem iguais (caso Lado-Ângulo-Lado);
- Se dois ângulos e o lado entre eles forem iguais (caso Ângulo-Lado-Ângulo);
- E no caso dos triângulos retângulos, se a hipotenusa e um dos catetos forem iguais.
Essas são regras que funcionam sempre e nos ajudam a comparar triângulos com segurança.
Onde usamos isso na vida real?
A congruência de triângulos aparece em muitos lugares:
- Na engenharia e na arquitetura, para garantir que peças de estruturas se encaixem perfeitamente;
- Na construção civil, quando é preciso fazer paredes, telhados e rampas com medidas exatas;
- Na arte e nos mosaicos, que usam figuras geométricas repetidas de forma precisa;
- Na confecção de roupas e calçados, onde moldes iguais precisam ser reproduzidos várias vezes.
Até a natureza nos mostra congruência! Muitas folhas, asas de insetos e flores apresentam formas triangulares que se repetem com perfeição.
Para revisar esse conteúdo, assista à videoaula da professora Cristiane Souza, “Triângulos: conceito e classificações“, no Canal Estúdio Conexão Escola, no YouTube.
Agora, resolva as atividades propostas a seguir.
QUESTÃO 1
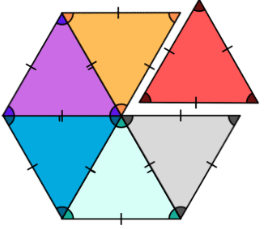
Observe a imagem a seguir. Nela existem pares de triângulos congruentes e sua tarefa é identificá-los, seguindo os casos de congruência.
Agora, preencha a tabela com os dados faltantes.
| Caso de congruência | Par de triângulos congruentes |
| L L L (lado, lado, lado) | |
| L A L (lado, ângulo, lado) | |
| A L A (ângulo, lado, ângulo) |
QUESTÃO 2
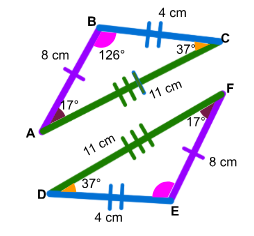
Os triângulos ABC e CDE são congruentes.
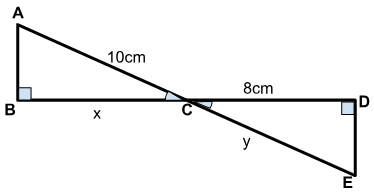
Logo, as medidas de x e y são, nesta ordem, iguais a
(A) 10 cm e 6 cm.
(B) 4 cm e 5 cm.
(C) 8 cm e 6 cm.
(D) 8 cm e 10 cm.
QUESTÃO 3
O triângulo ABC a seguir é isósceles.
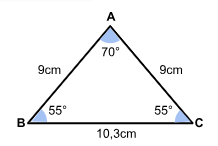
Agora,
I) escolha um dos casos de congruência de triângulos;
II) desenhe um triângulo congruente a este com base no caso de congruência escolhido;
III) em seguida, escreva um breve parágrafo explicando porque o seu desenho é congruente ao triângulo original.
QUESTÃO 4
O triângulo ABC é equilátero. O segmento AM é a altura desse triângulo e o dividiu em dois outros triângulos: AMB e AMC.
Podemos afirmar que os triângulos AMB e AMC são congruentes? Justifique a sua resposta (use os casos de congruência para justificar sua resposta).
QUESTÃO 5
Uma empresa tem como logotipo, dois triângulos. Estes triângulos são retângulos, cujas medidas, em centímetros, estão descritas na imagem abaixo.
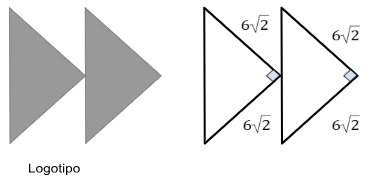
O caso de congruência que justifica dizer que os dois triângulos do logotipo são congruentes é o
(A) LLL (lado, lado, lado).
(B) LAL (lado, ângulo, lado).
(C) ALA (ângulo, lado, ângulo).
(D) AAA (ângulo, ângulo, ângulo).
| Autoria: | Cristiane Soares de Souza |
| Formação: | Matemática – Licenciatura. |
| Componente Curricular: | Matemática. |
| Habilidades: | (EF08MA14-B) Identificar triângulos congruentes seguindo os critérios de congruência de triângulos. |
| Descritor: | D3 – Identificar propriedades de triângulos pela comparação de medidas de lados e ângulos. |
| Objetos de conhecimento: | Triângulos, classificação dos triângulos, critérios de congruência entre triângulos. |
| Referência: | Araribá mais: Matemática: organizadora Editora Moderna, obra coletiva concebida, desenvolvida e produzida pela Editora Moderna. Editores responsáveis: Mara Regina Garcia Gay, Willian Raphael Silva. 1ª Edição, São Paulo, 2018. EUGÊNIO, Robson da Silva. Letramento probabilístico nos anos finais do ensino fundamental: um processo de formação dialógica com professores de matemática. / Eugênio Robson da Silva. – Recife, 2019. Disponível em URL https://repositorio.ufpe.br/handle/123456789/38245, consultado em 10/03/2025. |