Esta proposta de atividade de Matemática, elaborada com base no DC/GO – Ampliado, é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Casos de semelhança entre triângulos
O triângulo é um polígono particular dada a sua rigidez geométrica. Isso significa que, se fixarmos o comprimento dos seus lados ou os seus ângulos, sua forma não muda. Tomemos como exemplo o triângulo ABC a seguir.
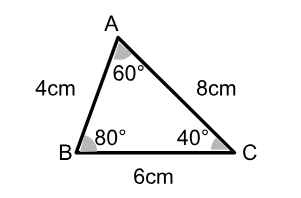
Um triângulo com lados 4cm, 6cm e 8cm terá esta forma e os ângulos medirão 40°, 60° e 80°. Por ser um polígono rígido, se aumentarmos ou reduzirmos as suas dimensões de forma proporcional, a forma se mantém e as medidas de ângulo também. Sendo assim, os polígonos serão semelhantes: mesma forma, mesmos ângulos e lados proporcionais.
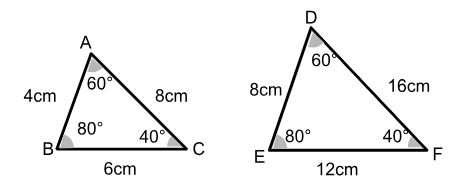
Por causa dessa rigidez, os triângulos possuem critérios específicos que permitem identificar semelhanças observando apenas alguns de seus elementos. Esses critérios são chamados de casos de semelhança.
Critérios de semelhança de triângulos
- Caso AA (Ângulo-Ângulo): Se dois ângulos de um triângulo forem congruentes a dois ângulos de outro triângulo, então esses triângulos são semelhantes. Como a soma dos ângulos internos de qualquer triângulo é sempre 180°, bastam dois ângulos iguais para garantir a semelhança.
- Caso LAL (Lado-Ângulo-Lado): Se dois lados de um triângulo forem proporcionais a dois lados de outro triângulo, e o ângulo entre esses lados for congruente, então os triângulos são semelhantes.
- Caso LLL (Lado-Lado-Lado): Se os três lados de um triângulo forem proporcionais aos três lados de outro triângulo, então esses triângulos são semelhantes.
Aplicações da semelhança de triângulos
A semelhança de triângulos tem diversas aplicações práticas, como:
- Medir a altura de prédios ou árvores usando a projeção da sombra e a proporção entre triângulos semelhantes.
- Determinar distâncias inacessíveis em mapas, por meio de triangulação.
- Resolver problemas de escalas em desenhos técnicos e plantas arquitetônicas.
Rigidez geométrica do triângulo
Para entender melhor a relação entre a rigidez geométrica do triângulo e como isto interfere na semelhança entre triângulos, assista à videoaula “Rigidez geométrica e a semelhança entre triângulos“, disponível no canal Estúdio Conexão Escola, no YouTube.
Agora, resolva as questões a seguir.
QUESTÃO 1
Na imagem a seguir, todos os triângulos são isósceles.
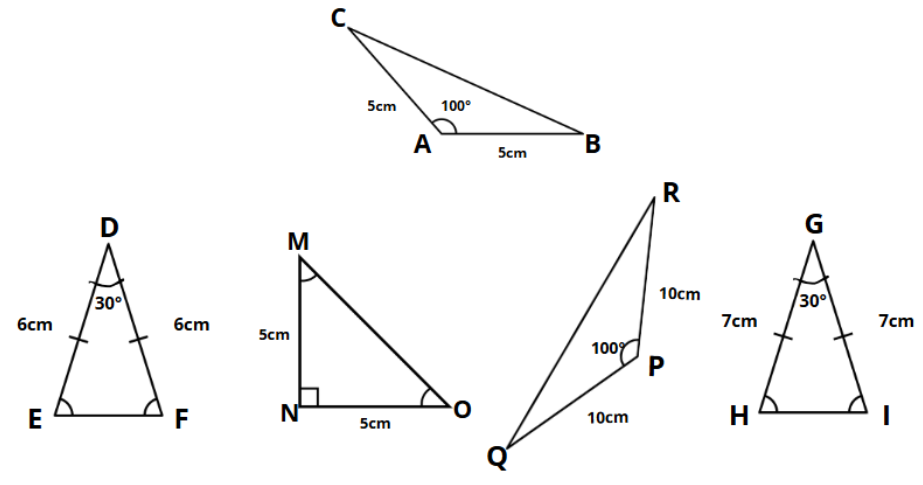
Considerando o caso de semelhança lado, ângulo, lado, apenas um dos triângulos é semelhante ao triângulo ABC. Este triângulo é o
(A) DEF
(B) MNO
(C) PQR
(D) GHI
QUESTÃO 2
Os triângulos ABC e DEC são semelhantes.
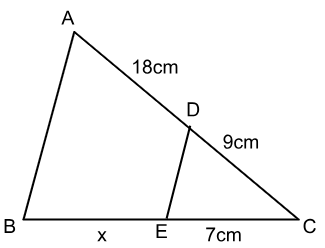
Calcule a medida do segmento BE.
QUESTÃO 3
Um prédio de 7,2 m de altura projeta uma sombra de 13,5 m de comprimento. No mesmo momento, uma pessoa de 1,80m de altura, está próxima ao prédio e projeta uma sombra de (A) 2 m
(B) 5 m
(C) 7 m
(D) 10 m
QUESTÃO 4
Os triângulos ABC e CDE são semelhantes.
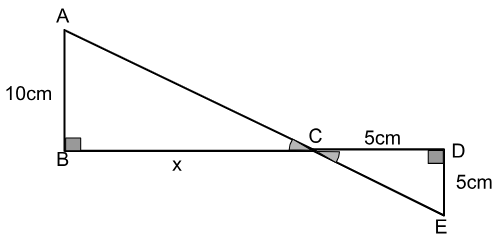
Calcule a medida de x.
QUESTÃO 5
Os triângulos ABC e DEF são semelhantes. A razão de semelhança entre os lados desses triângulos é de 2:3.
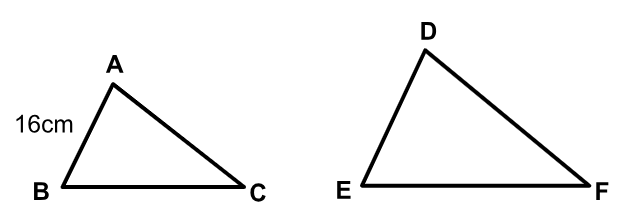
Se AB= 16cm, calcule a medida do segmento DE.
QUESTÃO 6
Um grupo de estudantes, em uma atividade de Matemática, decidiu medir a altura do prédio da escola utilizando a semelhança entre triângulos. Para isso, escolheram um dos colegas e mediram a altura desse estudante e o comprimento das sombras projetadas pelo prédio e pelo estudante no mesmo momento. As medidas estão na imagem a seguir.
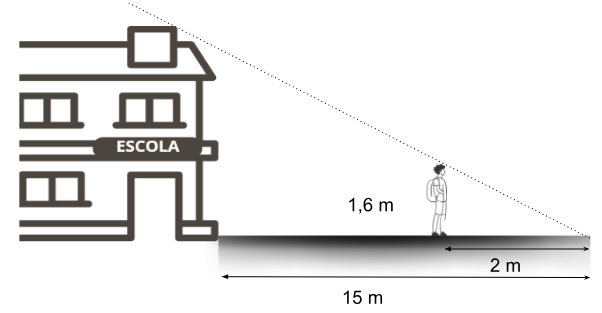
Com base nessas informações, calcule a altura da escola.
| Autoria: | Cristiane Soares de Souza |
| Formação: | Matemática – Licenciatura |
| Componente Curricular: | Matemática |
| Habilidade(s): | (EF09MA12-B) Reconhecer triângulos semelhantes em situações de ampliação, congruência e redução, e as relações que existem entre seus perímetros e suas áreas. |
| Descritor: | D5 – Reconhecer a conservação ou modificação de medidas de lado, do perímetro, da área na ampliação e/ou redução de figuras poligonais usando malhas quadriculadas. |
| Objetos de conhecimento: | Ampliação e redução de polígonos na malha quadriculada, conservação e modificação de medidas na ampliação e redução de polígonos (perímetro e área), semelhança de triângulos, casos de semelhanças de triângulos. |
| Referência: | SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo, Moderna, 2018. PEREIRA, Marcos Fabrício Ferreira. Uma Sequência Didática para o ensino de Semelhança de Figuras Planas. XX Ebrapen – Encontro Brasileiro de Pós-graduação em Educação Matemática, 2016. Disponível em http://www.ebrapem2016.ufpr.br/wp-content/uploads/2016/04/gd2_Marcos_Fabricio.pdf, consultado em 17/03/2025. |

